
【题目】已知![]() .
.
(1)判断函数![]() 的奇偶性并证明;
的奇偶性并证明;
(2)证明![]() 是定义域内的增函数;
是定义域内的增函数;
(3)解不等式![]() .
.
【答案】(1)奇函数,证明详见解析;(2)增函数,证明详见解析;(3)![]() 。
。
【解析】
试题分析:(1)函数![]() 的定义域为R,关于原点对称,
的定义域为R,关于原点对称,![]() ,验证
,验证![]() 的值,
的值,![]() ,所以即
,所以即![]() ,因此函数
,因此函数![]() 为奇函数;
为奇函数;
(2)首先可以将函数化简,即![]() ,根据定义证明函数
,根据定义证明函数![]() 在定义域内为增函数,设
在定义域内为增函数,设![]() 是R上任意两个不等的实数,且
是R上任意两个不等的实数,且![]() ,则
,则![]() ,
,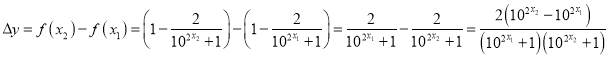 ,由于函数
,由于函数![]() 在R上为增函数,所以当
在R上为增函数,所以当![]() 时,
时,![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() ,则函数
,则函数![]() 在R上为增函数;(3)由第(1)、(2)问可知函数
在R上为增函数;(3)由第(1)、(2)问可知函数![]() 为奇函数且为增函数,所以
为奇函数且为增函数,所以![]() 转化为
转化为![]() ,即
,即![]() ,所以转化为
,所以转化为![]() ,所以
,所以![]() ,
,![]() ,则
,则![]() 。
。
试题解析:(1)∵![]() 的定义域为R,且
的定义域为R,且![]() ,
,
∴![]() 是奇函数.
是奇函数.
(2)![]()
![]()
![]()
设![]() 且
且![]() ,则
,则
![]()
![]()
![]()
∵![]() 为增函数,∴当
为增函数,∴当![]() 时,
时,![]() ,
,
又∵![]() , ∴
, ∴![]() ,即
,即![]()
∴![]() 在定义域上为增函数.
在定义域上为增函数.
(3) 不等式可化为![]()
由(1)知![]() 是奇函数 ∴
是奇函数 ∴![]()
由(2)知![]() 在定义域上为增函数 ∴
在定义域上为增函数 ∴![]()
解得![]()


科目:高中数学 来源: 题型:
【题目】某服装厂生产一种服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购超过100件时,每多订购1件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设销售一次订购![]() 件,服装的实际出厂单价为
件,服装的实际出厂单价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)若![]() ,求函数
,求函数![]() 的表达式;
的表达式;
(2)在(1)的条件下,设函数![]() ,若
,若![]() 上是单调函数,求实数
上是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)是否存在![]() 使得函数
使得函数![]() 在
在![]() 上的最大值是4?若存在,求出
上的最大值是4?若存在,求出![]() 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={0,1,2,3},B={x|x(x﹣3)<0},则A∩B=( )
A.{0,1,2,3}
B.{0,1,2}
C.{1,2}
D.{1,2,3}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com