Question

已知O为原点，有点A（d,0）、B（0，d），其中d>0，点P在线段AB上，且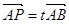（0≤t≤1），则的最大值为________________．

Answer 1

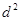
解析试题分析：首先分析题目已知A、B的坐标，点P在线段AB上，且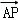=t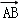（0≤t≤1），求•的最大值．故可考虑根据向量的坐标及加减运算表示出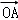与．然后根据平面向量的数量乘积运算求出结果即可．解：因为点A、B的坐标分别为（d，0），（0，d）
所以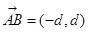 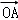，=（d，0）又由点P在线段AB上，且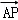=t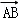=（﹣dt，dt）
所以=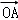+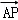=（a，0）+（﹣at，at）=（﹣dt+d，dt）,则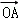•=（d，0）•（﹣dt+d，at）=﹣d²t+d²，当t=0时候取最大为d²．故答案为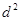
考点：平面向量的数量积
点评：此题主要考查平面向量的数量乘积的运算问题，其中涉及到向量的坐标表示及加法运算，题目覆盖知识点少，属于基础题目．