
【题目】某学校艺术专业300名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
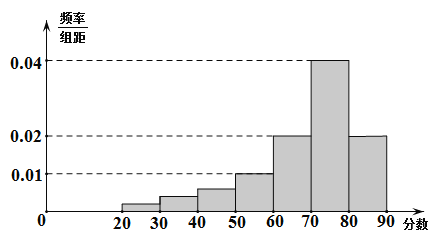
(1)从总体的300名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
【答案】(1)0.4 (2)15人 (3)3∶2
【解析】
(1)根据频率分布直方图求出样本中分数小于70的频率,用频率估计概率值;
(2)计算样本中分数小于50的频率和频数,估计总体中分数在区间![]() ,
,![]() 内的人数;
内的人数;
(3)由题意计算样本中分数不小于70的学生人数以及男生、女生人数,求男生和女生人数的比例.
解:(1)根据频率分布直方图可知,样本中分数不小于70的频率为(0.02+0.04)×10=0.6,
所以样本中分数小于70的频率为1-0.6=0.4.
所以从总体的300名学生中随机抽取一人,其分数小于70的概率估计值为0.4.
(2)根据题意,样本中分数不小于50的频率为 (0.01+0.02+0.04+0.02)×10=0.9,
故样本中分数小于50的频率为0.1,
故分数在区间[40,50)内的人数为100×0.1-5=5.
所以总体中分数在区间[40,50)内的人数估计为![]() .
.
(3)由题意可知,样本中分数不小于70的学生人数为
(0.02+0.04)×10×100=60,
所以样本中分数不小于70的男生人数为![]() .
.
所以样本中的男生人数为30×2=60,
女生人数为100-60=40,
男生和女生人数的比例为60∶40=3∶2.
所以根据分层抽样原理,总体中男生和女生人数的比例估计为3∶2.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某商场从2018年1月份起的前这个月,顾客对某商品的需求总量,![]() (单位:件)与x的关系近似地满足
(单位:件)与x的关系近似地满足![]() (其中
(其中![]() ,且
,且![]() ),该商品第x月的进货单价
),该商品第x月的进货单价![]() (单位:元)与x的近似关系是
(单位:元)与x的近似关系是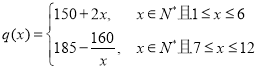 .
.
(1)写出2018年第x月的需求量![]() (单位:件)与x的函数关系式;
(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2018年第几个月销售该商品的月利润![]() 最大,最大月利润为多少元?
最大,最大月利润为多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面相交于
所在平面相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点, ![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点,
的点, ![]() .
.
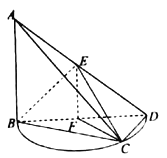
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 为半圆弧
为半圆弧![]() 上的一个三等分点(靠近点
上的一个三等分点(靠近点![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种水果按照果径大小可分为四类:标准果、优质果、精品果、礼品果.某采购商从采购的一批水果中随机抽取![]() 个,利用水果的等级分类标准得到的数据如下:
个,利用水果的等级分类标准得到的数据如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
个数 | 10 | 30 | 40 | 20 |
(1)若将频率是为概率,从这![]() 个水果中有放回地随机抽取
个水果中有放回地随机抽取![]() 个,求恰好有
个,求恰好有![]() 个水果是礼品果的概率.(结果用分数表示)
个水果是礼品果的概率.(结果用分数表示)
(2)用样本估计总体,果园老板提出两种购销方案给采购商参考.
方案![]() :不分类卖出,单价为
:不分类卖出,单价为![]() 元
元![]() .
.
方案![]() :分类卖出,分类后的水果售价如下:
:分类卖出,分类后的水果售价如下:
等级 | 标准果 | 优质果 | 精品果 | 礼品果 |
售价(元/kg) | 16 | 18 | 22 | 24 |
从采购单的角度考虑,应该采用哪种方案?
(3)用分层抽样的方法从这![]() 个水果中抽取
个水果中抽取![]() 个,再从抽取的
个,再从抽取的![]() 个水果中随机抽取
个水果中随机抽取![]() 个,
个,![]() 表示抽取的是精品果的数量,求
表示抽取的是精品果的数量,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设函数f(x)=alnx﹣bx2(x>0).
(1)若函数f(x)在x=1处于直线![]() 相切,求函数f(x)在
相切,求函数f(x)在![]() 上的最大值;
上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,求实数m的取值范围.
],x∈[1,e2]都成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com