
分析 (1)当a=2时,解不等式|2x+2|-2≤6得-5≤x≤3,即可求不等式f(x)≤6的解集;
(2)当x∈R时,f(x)+g(x)=|2x+a|-a+|2x-1|≥|2x+a+1-2x|-a=|a+1|-a,当$x=\frac{1}{2}$时等号成立,所以当x∈R时f(x)+g(x)≥3等价于|a+1|-a≥3,即可求a的取值范围.
解答 解:(1)当a=2时,f(x)=|2x+2|-2
解不等式|2x+2|-2≤6得-5≤x≤3
因此不等式f(x)≤6的解集为{x|-5≤x≤3}…(5分)
(2)当x∈R时,f(x)+g(x)=|2x+a|-a+|2x-1|≥|2x+a+1-2x|-a=|a+1|-a
当$x=\frac{1}{2}$时等号成立,所以当x∈R时f(x)+g(x)≥3等价于|a+1|-a≥3
当a≤-1时,a≤-2
当a>-1时,无解,
所以a∈(-∞,-2]…(10分)
点评 本题考查绝对值不等式的解法,考查绝对值不等式,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
| 愿意参加 | 不愿意参加 | 合计 | |
| 城填生 | 50 | 25 | 75 |
| 农村生 | 10 | 15 | 25 |
| 合计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
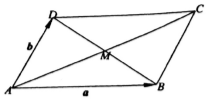
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ | B. | -$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | C. | $\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{2}$$\overrightarrow{b}$ | D. | -$\frac{1}{2}$$\overrightarrow{a}$+$\frac{1}{2}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com