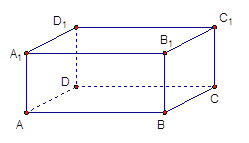
[题目]长方体中.(1)求直线与所成角,(2)求直线与平面所成角的正弦. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】长方体中，

（1）求直线与所成角；

（2）求直线与平面所成角的正弦.

【答案】（1）直线所成角为90°；（2）。

【解析】

试题（1）建立空间直角坐标系，求出直线AD1与B1D的方向向量，利用向量的夹角公式，即可求直线AD1与B1D所成角；

（2）求出平面B1BDD1的法向量，利用向量的夹角公式，即可求直线AD1与平面B1BDD1所成角的正弦．

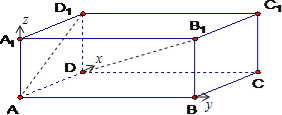
解：（1）建立如图所示的直角坐标系，则A（0，0，0），D1（1，0，1），B1（0，2，1），D（1，0，0）．

∴，

∴cos==0，

∴=90°，

∴直线AD1与B1D所成角为90°；

（2）设平面B1BDD1的法向量=（x，y，z），则

∵，=（﹣1，2，0），

∴，

∴可取=（2，1，0），

∴直线AD1与平面B1BDD1所成角的正弦为=．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知△ABC的内角A，B，C所对边分别为a、b、c，且2acosC=2b-c．

（1）求角A的大小；

（2）若AB=3，AC边上的中线SD的长为，求△ABC的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在某中学举行的电脑知识竞赛中，将高一年级两个班参赛的学生成绩进行整理后分成五组，绘制如图所示的频率分布直方图.已知图中从左到右的第一，第三，第四，第五小组的频率分别是0.30，0.15，0.10，0.05，第二小组的频数是40.

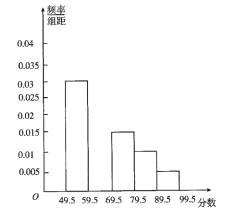
（1）补齐图中频率分布直方图，并求这两个班参赛学生的总人数；

（2）利用频率分布直方图，估算本次比赛学生成绩的平均数和中位数.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将所有的正奇数按以下规律分组，第一组：1；第二组：3，5，7；第三组：9，11，13，15，17；… 表示n是第i组的第j个数，例如，，则（）

A.B.C.D.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】将下列问题的解答过程补充完整．

依次计算数列，，，，…的前四项的值，由此猜测的有限项的表达式，并用数学归纳法加以证明．

解：计算，

，

① ，

② ，

由此猜想 ③ ．（*）

下面用数学归纳法证明这一猜想．

（i）当时，左边，右边，所以等式成立．

（ⅱ）假设当时，等式成立，即

④ ．

那么，当时，

⑤

⑥

⑦ ．

等式也成立．

根据（i）和（ⅱ）可以断定，（*）式对任何都成立．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列说法正确的是( )

A. “f(0)”是“函数f（x）是奇函数”的充要条件

B. 若p：，，则：，

C. “若，则”的否命题是“若，则”

D. 若为假命题，则p，q均为假命题

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某地某高中2018年的高考考生人数是2015年高考考生人数的1.5倍.为了更好地对比该校考生的升学情况，统计了该校2015和2018年高考情况，得到如下饼图：

2018年与2015年比较，下列结论正确的是（）

A. 一本达线人数减少

B. 二本达线人数增加了0.5倍

C. 艺体达线人数相同

D. 不上线的人数有所增加

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为．如果，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为，即取出的每件产品是优质品的概率都为，且各件产品是否为优质品相互独立．