Question

6．己知线段AB两端点的坐标分别为A（-1，2），B（4，3），若直线1：mx+y-2m=0与线段AB有交点，求实数m的取值范围．

Answer 1

分析 由直线l的方程可得直线过定点P（2，0），作出图形，求出P与线段两端点连线的斜率，则m值可求．

解答 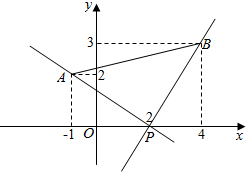解：由直线1：mx+y-2m=0，得m（x-2）+y=0，∴直线l过定点P（2，0），
若直线1：mx+y-2m=0与线段AB有交点，如图，
∵${k}_{PA}=\frac{2}{-1-2}=-\frac{2}{3}，{k}_{PB}=\frac{3-0}{4-2}=\frac{3}{2}$，
∴-m$≤-\frac{2}{3}$或-m$≥\frac{3}{2}$，即m$≥\frac{2}{3}$或m$≤-\frac{3}{2}$．
故实数m的取值范围是（-∞，$-\frac{3}{2}$]∪[$\frac{2}{3}，+∞$）．

点评 本题考查直线的斜率，考查了数形结合的解题思想方法，是中档题．