
分析 利用余弦定理求出BC的长,进而由正弦定理求出平面ABC截球所得圆的半径,结合球心距,求出球的半径,代入球的表面积公式,可得答案.
解答 解:在△ABC中,
∵AB=AC=2,∠BAC=120°,
∴BC=$\sqrt{4+4-2×2×2×(-\frac{1}{2})}$=2$\sqrt{3}$,
由正弦定理可得平面ABC截球所得圆的半径(即△ABC的外接圆半径),
r=$\frac{2\sqrt{3}}{2×\frac{\sqrt{3}}{2}}$=2,
又∵球心到平面ABC的距离d=$\frac{1}{2}$R,
∴球O的半径R=$\sqrt{4+\frac{1}{4}{R}^{2}}$,
∴R2=$\frac{16}{3}$,
故球O的表面积S=4πR2=$\frac{64}{3}π$,
故答案为$\frac{64}{3}π$.
点评 本题考查的知识点是球的体积和表面积,其中根据已知条件求出球的半径是解答本题的关键.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | [-2,2] | C. | (-∞,-4)∪(4,+∞) | D. | [-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x0∈R,${x_0}^2-2{x_0}+1≥0$ | B. | 存在x0∈R,${x_0}^2-2{x_0}+1≤0$ | ||
| C. | 存在x0∈R,${x_0}^2-2{x_0}+1<0$ | D. | 对任意的x∈R,x2-2x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 212-57 | B. | 211-47 | C. | 210-38 | D. | 29-30 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
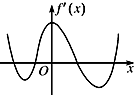
| A. | 无极大值点,有四个极小值点 | B. | 有三个极大值点,两个极小值点 | ||
| C. | 有两个极大值点,两个极小值点 | D. | 有四个极大值点,无极小值点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com