考点:点、线、面间的距离计算,平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)分别连结B1D1、ED、FB,由正方体性质知B1D1∥BD.由此能证明E、F、B、D四点共面.
(2)连结A1C1交MN于P点,交EF于点Q,连结AC交BD于点O,分别连结PA、QO.由已知得四边形PAOQ为平行四边形,由此能证明平面AMN∥平面EFBD.
(3)过A1作A1H⊥AP,则MN⊥A1H,A1H⊥平面AMN,由此能求出点A1到平面AMN的距离.
解答:
(1)证明:分别连结B
1D
1、ED、FB,由正方体性质知B
1D
1∥BD.
∵E、F分别是D
1C
1和B
1C
1的中点,
∴EF
B
1D
1.∴EF
BD.
∴E、F、B、D四点共面.
(2)证明:连结A
1C
1交MN于P点,交EF于点Q,
连结AC交BD于点O,分别连结PA、QO.
∵M、N为A
1B
1、A
1D
1的中点,
∴MN∥EF.而EF?面EFBD.
∴MN∥面EFBD.∵PQ
AO,
∴四边形PAOQ为平行四边形.∴PA∥QO.
而QO?平面EFBD,∴PA∥平面EFBD,
且PA∩MN=P,PA、MN?面AMN.
∴平面AMN∥平面EFBD.
(3)解:∵A
1B
1C
1D
1是正方形,M、N分别为棱A
1B
1、A
1D
1的中点,
∴A
1P⊥MN,A
1P=
A1C1=
a,
∵正方体ABCD-A
1B
1C
1D
1中,AA
1⊥平面A
1B
1C
1D
1,
∴MN⊥AA
1,又AA
1∩A
1P=A
1,∴MN⊥平面AA
1P,
过A
1作A
1H⊥AP,则MN⊥A
1H,∴A
1H⊥平面AMN,
∵AP=
=
a,
又
AP×A1H=AA1×A1P,
∴
A1H==
=
.
∴点A
1到平面AMN的距离为
.
点评:本题考查B、D、E、F四点共面的证明,考查平面AMN∥平面EFBD的证明,考查点A1到平面AMN的距离的求法,解题时要认真审题,注意向量法的合理运用.

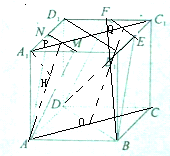
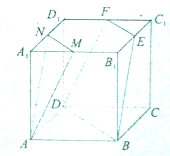 棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.
棱长为a的正方体ABCD-A1B1C1D1中,M、N、E、F分别为棱A1B1、A1D1、C1D1、B1C1的中点.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案