
【题目】已知函数![]() .
.
(1)求曲线![]() 在点(
在点(![]() )处的切线方程;
)处的切线方程;
(2)证明:当![]() 时,
时,![]() 。
。
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)![]() ,由f′(0)=2,可得切线斜率k=2,即可得到切线方程;
,由f′(0)=2,可得切线斜率k=2,即可得到切线方程;
(2)可得![]() =﹣
=﹣![]() .可得f(x)在(﹣
.可得f(x)在(﹣![]() ),(2,+∞)递减,在(﹣
),(2,+∞)递减,在(﹣![]() ,2)递增,注意到a≥1时,函数g(x)=ax2+x﹣1在(2,+∞)单调递增,且g(2)=4a+1>0,只需(x)
,2)递增,注意到a≥1时,函数g(x)=ax2+x﹣1在(2,+∞)单调递增,且g(2)=4a+1>0,只需(x)![]() ≥﹣e,即可.
≥﹣e,即可.
(1)![]() =﹣
=﹣![]() .
.
∴f′(0)=2,即曲线y=f(x)在点(0,﹣1)处的切线斜率k=2,
∴曲线y=f(x)在点(0,﹣1)处的切线方程方程为y﹣(﹣1)=2x.
即2x﹣y﹣1=0为所求.
(2)证明:函数f(x)的定义域为:R,
可得![]() =﹣
=﹣![]() .
.
令f′(x)=0,可得![]() ,
,
当x![]() 时,f′(x)<0,x
时,f′(x)<0,x![]() 时,f′(x)>0,x∈(2,+∞)时,f′(x)<0.
时,f′(x)>0,x∈(2,+∞)时,f′(x)<0.
∴f(x)在(﹣![]() ),(2,+∞)递减,在(﹣
),(2,+∞)递减,在(﹣![]() ,2)递增,
,2)递增,
注意到a≥1时,函数g(x)=ax2+x﹣1在(2,+∞)单调递增,且g(2)=4a+1>0
函数f(x)的图象如下:
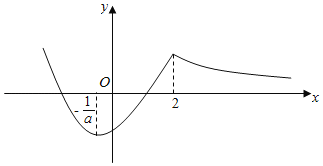
∵a≥1,∴![]() ,则
,则![]() ≥﹣e,
≥﹣e,
∴f(x)![]() ≥﹣e,
≥﹣e,
∴当a≥1时,f(x)+e≥0.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面几何中,与三角形的三条边所在直线的距离相等的点有且只有四个.类似的:在立体几何中,与正四面体的六条棱所在直线的距离相等的点 ( )
A. 有且只有一个 B. 有且只有三个 C. 有且只有四个 D. 有且只有五个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下资料是一位销售经理收集到的每年销售额y(千元)和销售经验x(年)的关系:
销售经验x/年 | 1 | 3 | 4 | 4 | 6 | 8 | 10 | 10 | 11 | 13 |
年销售额y/千元 | 80 | 97 | 92 | 102 | 103 | 111 | 119 | 123 | 117 | 136 |
(1)依据这些数据画出散点图并作直线![]() =78+4.2x,计算
=78+4.2x,计算![]() ;
;
(2)依据这些数据求回归直线方程并据此计算![]() ;
;
(3)比较(1) (2)中的残差平方和![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚疼减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起脚疼每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了?”根据此规律,求后3天一共走多少里( )
A.156里
B.84里
C.66里
D.42里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在常数![]() ,使得数列
,使得数列![]() 满足
满足![]() 对一切
对一切![]() 恒成立,则称
恒成立,则称![]() 为“可控数列”.
为“可控数列”.
(1) 若数列![]() 的通项公式为
的通项公式为![]() ,试判断数列
,试判断数列![]() 是否为“可控数列”?并说明理由;
是否为“可控数列”?并说明理由;
(2) 若![]() 是首项为5的“可控数列”,且单调递减,问是否存在常数
是首项为5的“可控数列”,且单调递减,问是否存在常数![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3) 若“可控数列”![]() 的首项为2,
的首项为2,![]() ,求
,求![]() 不同取值的个数及最大值.(直接写出结果)
不同取值的个数及最大值.(直接写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,斜边
,斜边![]() 可以通过
可以通过![]() 以直线
以直线![]() 为轴旋转得到,且二面角
为轴旋转得到,且二面角![]() 是直二面角,动点
是直二面角,动点![]() 在斜边
在斜边![]() 上.
上.
(1)当D为AB的中点时,求异面直线AO与CD所成角的正切值;
(2)求CD与平面AOB所成角的正切值的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com