
【题目】已知点![]() ,圆
,圆![]() 的方程为
的方程为![]() ,点
,点![]() 为圆上的动点,过点
为圆上的动点,过点![]() 的直线
的直线![]() 被圆
被圆![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】[选修4-4 , 坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为 ![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为 ![]() (t为参数).(10分)
(t为参数).(10分)
(1)若a=﹣1,求C与l的交点坐标;
(2)若C上的点到l距离的最大值为 ![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汕头某通讯设备厂为适应市场需求,提高效益,特投入98万元引进世界先进设备奔腾6号,并马上投入生产.第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元.
请你根据以上数据,解决下列问题:(1)引进该设备多少年后,收回成本并开始盈利?(2)引进该设备若干年后,有两种处理方案:第一种:年平均盈利达到最大值时,以26万元的价格卖出;第二种:盈利总额达到最大值时,以8万元的价格卖出.问哪种方案较为合算?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1 , A2 , A3 , A4 , A5 , A6和4名女志愿者B1 , B2 , B3 , B4 , 从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.(12分)
(Ⅰ)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率.
(Ⅱ)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施。若实施方案一,预计第一年可以使出口额恢复到危机前的![]() 倍、
倍、![]() 倍、
倍、![]() 倍的概率分别为
倍的概率分别为![]() 、
、![]() 、
、![]() ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的![]() 倍、
倍、![]() 倍的概率分别为
倍的概率分别为![]() 、
、![]() 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的![]() 倍、
倍、![]() 倍、
倍、![]() 倍的概率分别为
倍的概率分别为![]() 、
、![]() 、
、![]() ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的![]() 倍、
倍、![]() 倍的概率分别为
倍的概率分别为![]() 、
、![]() 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令![]() 表示方案
表示方案![]() 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。
(1)写出![]() 的分布列;
的分布列;
(2)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(3)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为![]() 万元、
万元、![]() 万元、
万元、![]() 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln x-a(x-1),g(x)=ex.
(1)求函数f(x)的单调区间;
(2)若函数h(x)=f(x+1)+g(x),当x>0时,h(x)>1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
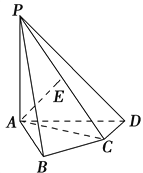
(1)证明:AE⊥平面PCD;
(2)求二面角A-PD-C的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com