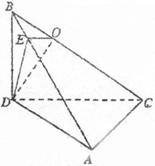
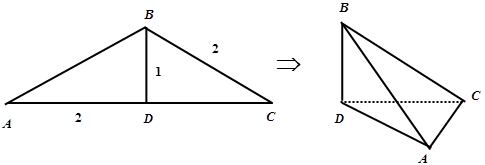如图,在
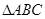
中,
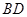
为
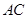
边上的高,
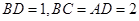
,沿
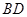
将
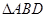
翻折,使得
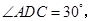
得几何体
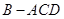
(1)求证:
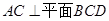
; (2)求二面角
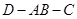
的余弦值。
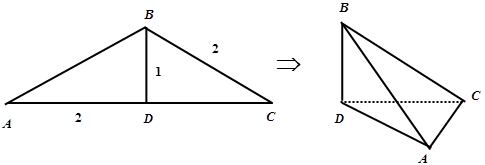
因为

,所以
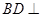
平面
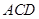
。
又因为
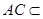
平面
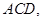
所以
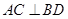
①……… 1分
在

中,
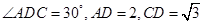
,由余弦定理,
得

因为
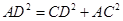
,所以
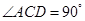
,即
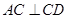
。② ……… 3分
由①,②及
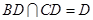
,可得
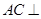
平面
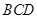
………4分
(2)在

中,过
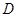
作
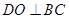
于

,则
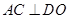
,所以
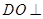
平面

在
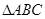
中,过

作
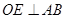
于
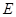
,连
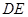
,则
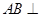
平面
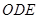
,
所以
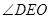
为二面角
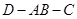
的平面角 ……… 6分
在
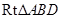
中,求得
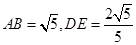
,
在
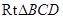
中,求得
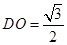
,
所以
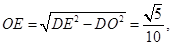
所以
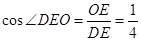
。
因此,所求二面角
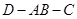
的余弦值为

。
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:填空题
已知向量
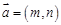
,
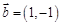
,其中
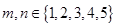
,则
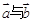
的夹角能成为直角三角形内角的概率是
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图四棱锥
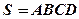
中,
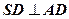
,
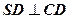
,
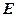
是
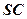
的中点,
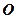
是底面正方形
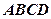
的中心,
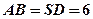
。
(Ⅰ)求证:
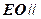
面
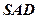
;
(Ⅱ)求直线
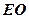
与平面
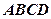
所成的角。

查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
若点A

关于

轴的对称点是B

,则

的值依次是( )
| A.1,-4,9 | B.2,-5,-8 | C.-3,-5,8 | D.2,5,8 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
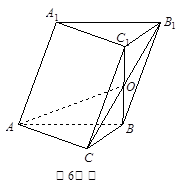
如图,在三棱柱
ABC-
A1B1C1中,
BC1与
B1C交于点
O,向量
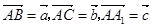
,则
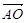
=
▲ .(试用
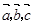
表示)
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在长方体
ABCD—
A1B1C1D1中,M为
AC与
BD的交点,若
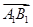
=
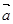
,

=
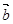
,
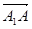
=
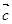
则下列向量中与
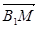
相等的向量是( )

查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知正方体
ABCD-
A1B1C1D1中,
E为侧面
BCC1B1的中心.若
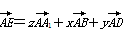
,则
x+
y+
z的值为( )
查看答案和解析>>

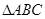 中,
中,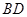 为
为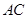 边上的高,
边上的高,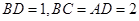 ,沿
,沿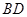 将
将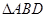 翻折,使得
翻折,使得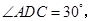 得几何体
得几何体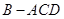
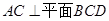 ; (2)求二面角
; (2)求二面角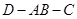 的余弦值。
的余弦值。