
【题目】已知函数 ![]() .
.
(1)函数f(x)在区间(0,+∞)上是增函数还是减函数?证明你的结论;
(2)当x>0时, ![]() 恒成立,求整数k的最大值;
恒成立,求整数k的最大值;
(3)试证明:(1+12)(1+23)(1+34)…(1+n(n+1))>e2n﹣3 .
【答案】
(1)解:由题 ![]() ,
,
故f(x)在区间(0,+∞)上是减函数;
(2)解:当x>0时, ![]() 恒成立,即
恒成立,即 ![]() 在(0,+∞)上恒成立,
在(0,+∞)上恒成立,
取 ![]() ,则
,则 ![]() ,
,
再取g(x)=x﹣1﹣ln(x+1),则 ![]() ,
,
故g(x)在(0,+∞)上单调递增,
而g(1)=﹣ln2<0,g(2)=1﹣ln3<0,g(3)=2﹣2ln2>0,
故g(x)=0在(0,+∞)上存在唯一实数根a∈(2,3),a﹣1﹣ln(a+1)=0,
故x∈(0,a)时,g(x)<0;x∈(a,+∞)时,g(x)>0,
故 ![]() ,故kmax=3
,故kmax=3
(3)证明:由(2)知: ![]() ,∴
,∴ ![]()
令 ![]() ,
,
又ln[(1+12)(1+23)(1+34)…(1+n(n+1))]=ln(1+1×2)+ln(1+2×3)+…+ln(1+n×(n+1)) ![]() =
= ![]()
即:(1+12)(1+23)(1+34)…[1+n(n+1)]>e2n﹣3
【解析】(1)求导函数,确定导数的符号,即可得到结论;(2)当x>0时, ![]() 恒成立,即
恒成立,即 ![]() 在(0,+∞)上恒成立,构造函数,求出函数的最小值,即可求整数k的最大值;(3)由(2)知:
在(0,+∞)上恒成立,构造函数,求出函数的最小值,即可求整数k的最大值;(3)由(2)知: ![]() ,从而令
,从而令 ![]() ,即可证得结论.
,即可证得结论.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减),还要掌握不等式的证明(不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等)的相关知识才是答题的关键.
在这个区间单调递减),还要掌握不等式的证明(不等式证明的几种常用方法:常用方法有:比较法(作差,作商法)、综合法、分析法;其它方法有:换元法、反证法、放缩法、构造法,函数单调性法,数学归纳法等)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某乐队参加一户外音乐节,准备从3首原创新曲和5首经典歌曲中随机选择4首进行演唱.
(1)求该乐队至少演唱1首原创新曲的概率;
(2)假定演唱一首原创新曲观众与乐队的互动指数为a(a为常数),演唱一首经典歌曲观众与乐队的互动指数为2a.求观众与乐队的互动指数之和 ![]() 的概率分布及数学期望.
的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosx(sinx﹣cosx)+m(m∈R),将y=f(x)的图象向左平移 ![]() 个单位后得到y=g(x)的图象,且y=g(x)在区间
个单位后得到y=g(x)的图象,且y=g(x)在区间 ![]() 内的最大值为
内的最大值为 ![]() .
.
(1)求实数m的值;
(2)在△ABC中,内角A、B、C的对边分别是a、b、c,若 ![]() ,且a+c=2,求△ABC的周长l的取值范围.
,且a+c=2,求△ABC的周长l的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以双曲线 ![]() (a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为正三角形,则该双曲线的离心率为( )
(a>0,b>0)上一点M为圆心的圆与x轴恰相切于双曲线的一个焦点F,且与y轴交于P、Q两点.若△MPQ为正三角形,则该双曲线的离心率为( )
A.4
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】体育课的排球发球项目考试的规则是:每位学生最多可发球3次,一旦发球成功,则停止发球,否则一直发到3次为止.设学生一次发球成功的概率为p (p≠0),发球次数为X,若X的数学期望EX>1.75,则p的取值范围是( )
A.(0, ![]() )
)
B.( ![]() ,1)
,1)
C.(0, ![]() )
)
D.( ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρsin(θ+
(θ为参数),以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρsin(θ+ ![]() )=2
)=2 ![]() (Ⅰ)直接写出C1的普通方程和极坐标方程,直接写出C2的普通方程;
(Ⅰ)直接写出C1的普通方程和极坐标方程,直接写出C2的普通方程;
(Ⅱ)点A在C1上,点B在C2上,求|AB|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
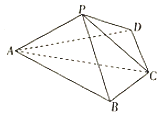
【题目】如图,四棱锥P﹣ABCD中,平面PAC⊥底面ABCD,BC=CD= ![]() AC=2,∠ACB=∠ACD=
AC=2,∠ACB=∠ACD= ![]() .
. 
(1)证明:AP⊥BD;
(2)若AP= ![]() ,AP与BC所成角的余弦值为
,AP与BC所成角的余弦值为 ![]() ,求二面角A﹣BP﹣C的余弦值..
,求二面角A﹣BP﹣C的余弦值..
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=[ax2﹣(2a+1)x+a+2]ex(a∈R).
(1)当a≥0时,讨论函数f(x)的单调性;
(2)设g(x)= ![]() ,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
,当a=1时,若对任意x1∈(0,2),存在x2∈(1,2),使f(x1)≥g(x2),求实数b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com