如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，点E在线段AD上，且CE∥AB.
(1)求证：CE⊥平面PAD；
(2)若PA＝AB＝1，AD＝3，CD＝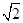
，∠CDA＝45°，求四棱锥P-ABCD的体积．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：解答题
如图，AB是圆O的直径，点C是弧AB的中点，点V是圆O所在平面外一点，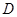
是AC的中点，已知
，
．
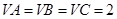（1）求证：AC⊥平面VOD；
（2）求三棱锥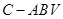
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，在四棱锥P－ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD,E为PD的中点，PA=2AB=2。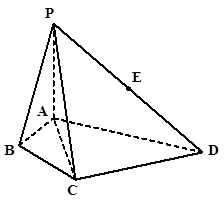
(1)求证：CE∥平面PAB;
(2)求四面体PACE的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图①所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4.如图②所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连结AB，设点F是AB的中点．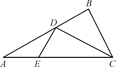
图①
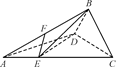图②
(1)求证：DE⊥平面BCD；
(2)若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥B-DEG的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图(1)所示,△ABC是等腰直角三角形,AC=BC=4,E、F分别为AC、AB的中点,将△AEF沿EF折起,使A′在平面BCEF上的射影O恰为EC的中点,得到图(2).
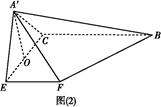
(1)求证:EF⊥A′C;
(2)求三棱锥F
A′BC的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.记CD=x,V(x)表示四棱锥F-ABCD的体积.
(1)求V(x)的表达式.
(2)求V(x)的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，四边形ABCD是边长为2的正方形，直线l与平面ABCD平行，E和F是l上的两个不同点，且EA＝ED，FB＝FC.E′和F′是平面ABCD内的两点，EE′和FF′都与平面ABCD垂直．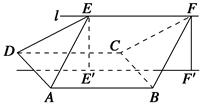
(1)证明：直线E′F′垂直且平分线段AD；
(2)若∠EAD＝∠EAB＝60 °，EF＝2.求多面体ABCDEF的体积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
,
，
，
沿
折叠成三棱锥，当三棱锥体积最大时，求此时三棱锥外接球的体积
是菱形，
是矩形，
面
,
．
；
，求四棱锥
的体积．