
【题目】已知曲线![]() 上的动点
上的动点![]() 满足到点
满足到点![]() 的距离比到直线
的距离比到直线![]() 的距离小1.
的距离小1.
(1)求曲线![]() 的方程;
的方程;
(2)动点![]() 在直线
在直线![]() 上,过点
上,过点![]() 分别作曲线
分别作曲线![]() 的切线
的切线![]() ,切点为
,切点为![]() .直线
.直线![]() 是否恒过定点,若是,求出定点坐标,若不是,请说明理由.
是否恒过定点,若是,求出定点坐标,若不是,请说明理由.
科目:高中数学 来源: 题型:
【题目】如图,已知![]() 的边
的边![]() 所在直线的方程为
所在直线的方程为![]() ,
,![]() 满足
满足![]() ,点
,点![]() 在
在![]() 边所在直线上且满足
边所在直线上且满足![]() .
.

(1)求![]() 边所在直线的方程;
边所在直线的方程;
(2)求![]() 外接圆的方程;
外接圆的方程;
(3)若动圆![]() 过点
过点![]() ,且与
,且与![]() 的外接圆外切,求动圆
的外接圆外切,求动圆![]() 的圆心的轨迹方程.
的圆心的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,已知曲线
轴的非负半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,它在点
,它在点![]() 处的切线为直线
处的切线为直线![]() .
.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)已知点![]() 为椭圆
为椭圆![]() 上一点,求点
上一点,求点![]() 到直线
到直线![]() 的距离的取值范围.
的距离的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左右焦点分别为
的左右焦点分别为![]() ,短轴两个端点为
,短轴两个端点为![]() ,且四边形
,且四边形![]() 是边长为2的正方形.
是边长为2的正方形.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 为椭圆长轴上一点,求
为椭圆长轴上一点,求![]() 的最大值与最小值;
的最大值与最小值;
(3)设![]() 是椭圆
是椭圆![]() 外的动点,满足
外的动点,满足![]() ,点
,点![]() 是线段
是线段![]() 与该椭圆的交点,点
与该椭圆的交点,点![]() 在线段
在线段![]() 上,并且满足
上,并且满足![]() ,
,![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克、米2).如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克、米2).如下表所示:

(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为
为![]() 上的偶函数,当
上的偶函数,当![]() 时,
时, ![]() .对于结论
.对于结论
(1)当![]() 时,
时, ![]() ;(2)函数
;(2)函数![]() 的零点个数可以为4,5,7;
的零点个数可以为4,5,7;
(3)若![]() ,关于
,关于![]() 的方程
的方程![]() 有5个不同的实根,则
有5个不同的实根,则![]() ;
;
(4)若函数![]() 在区间
在区间![]() 上恒为正,则实数
上恒为正,则实数![]() 的范围是
的范围是![]() .
.
说法正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P(万元)和Q(万元),它们与投入资金x(万元)的关系有经验公式:P=![]() ,Q=
,Q=![]()
![]() .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得的最大利润是多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少?能获得的最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量按照空气质量指数大小分为七档(五级),相对应空气质量的七个类别,指数越大,说明污染的情况越严重,对人体危害越大.
指数 | 级别 | 类别 | 户外活动建议 |
| Ⅰ | 优 | 可正常活动 |
| Ⅱ | 良 | |
| Ⅲ | 轻微污染 | 易感人群症状有轻度加剧,健康人群出现刺激症状,心脏病和呼吸系统疾病患者应减少体积消耗和户外活动. |
| 轻度污染 | ||
| Ⅳ | 中度污染 | 心脏病和肺病患者症状显著加剧,运动耐受力降低,健康人群中普遍出现症状,老年人和心脏病、肺病患者应减少体力活动. |
| 中度重污染 | ||
| Ⅴ | 重污染 | 健康人运动耐受力降低,由明显强烈症状,提前出现某些疾病,老年人和病人应当留在室内,避免体力消耗,一般人群应尽量减少户外活动. |
现统计邵阳市市区2016年1月至11月连续60天的空气质量指数,制成如图所示的频率分布直方图.
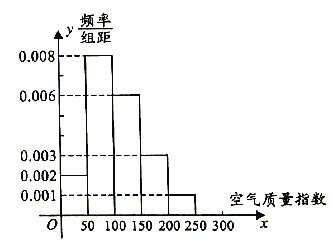
(1)求这60天中属轻度污染的天数;
(2)求这60天空气质量指数的平均值;
(3)一般地,当空气质量为轻度污染或轻度污染以上时才会出现雾霾天气,且此时出现雾霾天气的概率为![]() ,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
,请根据统计数据,求在未来2天里,邵阳市恰有1天出现雾霾天气的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com