
【题目】已知函数f(x)=lg(ax-bx)(a>1>b>0).
(Ⅰ)求f(x)的定义域;
(Ⅱ)当x∈(1,+∞)时,f(x)的值域为(0,+∞),且f(2)=lg2,求实数a、b的值.
【答案】(Ⅰ)(0,+∞)(Ⅱ)a=![]() ,b=
,b=![]()
【解析】
(Ⅰ)由ax﹣bx>0,(a>1>b>0)得![]() ,由此求得f(x)的定义域;
,由此求得f(x)的定义域;
(Ⅱ)令g(x)=ax﹣bx,可得x∈(1,+∞)时,g(x)>1.由g(1)=1,可得a﹣b=1 ①,又f(2)=lg2,故a2﹣b2=2 ②,由①②求得a、b的值.
解:(Ⅰ)由ax-bx>0,得ax>bx,
即![]() ,
,
∵a>1>b>0,∴![]() ,则x>0.
,则x>0.
∴f(x)的定义域为(0,+∞);
(Ⅱ)令g(x)=ax-bx,
∵a>1>b>0,∴g(x)在( 0,+∞)上为增函数.
由当x∈(1,+∞)时,f(x)的值域为(0,+∞),可得x∈(1,+∞)时,g(x)>1,
∴g(1)=1,可得a-b=1 ①,
又f(2)=lg2,∴a2-b2=2 ②,
联立①②得:a=![]() ,b=
,b=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知定义域为R的奇函数f(x),当x>0时,f(x)=ax2+bx+8(0<a<4),点A(2,0)在函数f(x)的图象上,且关于x的方程f(x)+1=0有两个相等的实根.
(1)求函数f(x)解析式;
(2)若x∈[t,t+2](t>0)时,函数f(x)有最小值1,求实数t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线, ![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,则
,则![]() ②若
②若![]() ,则
,则![]()
③若![]() ,则
,则![]() ④若
④若![]() ,则
,则![]()
其中正确命题的序号是( )
A. ①和② B. ②和③ C. ③和④ D. ①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为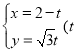 为参数),P、Q分别为直线
为参数),P、Q分别为直线![]() 与x轴、y轴的交点,线段PQ的中点为M.
与x轴、y轴的交点,线段PQ的中点为M.
(Ⅰ)求直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
轴的正半轴为极轴建立极坐标系,求点M的极坐标和直线OM的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出定理:三角形的外心、重心、垂心依次位于同一直线上,且重心到外心的距离是重心到垂心距离的一半![]() 这条直线被后人称之为三角形的欧拉线
这条直线被后人称之为三角形的欧拉线![]() 若
若![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 的欧拉线的方程为
的欧拉线的方程为![]() ,则顶点C的坐标为
,则顶点C的坐标为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2-x+m,且f(log2a)=m,log2f(a)=2,(a≠1).
(1)求a,m的值;
(2)求f(log2x)的最小值及对应的x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com