
 中,
中, 是
是 的中点,
的中点, ,
, ,且
,且 ,
, ,又
,又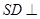 面
面 .
.
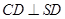 ;
; 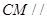 面
面 ;
;  的体积
的体积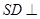 面
面 推出
推出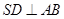 ,结合
,结合 得到
得到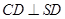 ;
; 中点
中点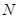 ,连结
,连结
 ,所以
,所以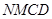 是平行四边形,
是平行四边形,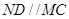 , 得到
, 得到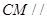 面
面 ;
;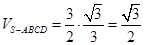
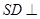 面
面 .,
.,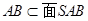 所以
所以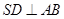 ---------------------2分
---------------------2分 所以
所以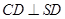 ---------------------4分
---------------------4分 中点
中点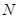 ,连结
,连结
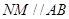 ,且
,且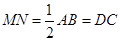 ,
,
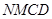 是平行四边形---------------------7分
是平行四边形---------------------7分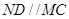 ,---------------------------------------8分
,---------------------------------------8分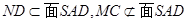
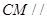 面
面 ;------------------9分
;------------------9分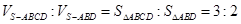 --------------------10分
--------------------10分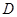 作
作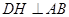 ,交于
,交于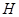 ,由题得
,由题得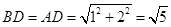 ---------11分
---------11分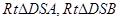 中,
中,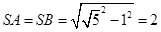 -------------------12分
-------------------12分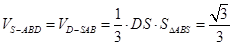 ------------------------13分
------------------------13分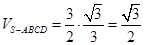 -------------------------14分
-------------------------14分

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com