
| A. | [2,+∞) | B. | (2,+∞) | C. | [$\sqrt{2}$,+∞) | D. | ($\sqrt{2}$,+∞) |
分析 求函数的导数,要使函数单调递增,则f′(x)≥0立,然后求出实数a的取值范围.
解答 解:因为f(x)=ex(cosx+a),所以f′(x)=ex(cosx+a-sinx).
要使函数单调递增,则f′(x)≥0成立.
即-sinx+a+cosx≥0恒成立.
所以a≥sinx-cosx,
因为sinx-cosx=$\sqrt{2}$sin(x-$\frac{π}{4}$)
所以-$\sqrt{2}$≤sinx-cosx≤$\sqrt{2}$,
所以a≥$\sqrt{2}$,
故选:C.
点评 本题主要考查导数的基本运算以及利用导数研究函数的单调性,注意当函数单调递增时,f'(x)≥0恒成立.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
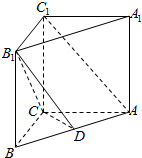 直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.
直棱柱ABC-A1B1C1中,AB=5,AC=4,BC=3,AA1=4,点D在AB上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
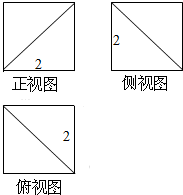
| A. | 18 | B. | 20 | C. | $18+2\sqrt{3}$ | D. | $18+4\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{100},1)$ | B. | (0,$\frac{1}{100}$)∪(1,+∞) | C. | $(\frac{1}{100},100)$ | D. | (0,1)∪(100,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | ?p∧?q | C. | ?p∧q | D. | p∧?q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com