Question

已知定点A(－1，0)、B(1，0)，动点M满足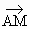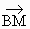：·等于点M到点C(0，1)距离平方的k倍．

(Ⅰ)试求动点M的轨迹方程，并说明方程所表示的曲线；

(Ⅱ)(文)当k＝2时，求|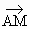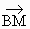＋|最大值和最小值．

(理)当k＝2时，求|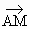＋2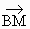|最大值和最小值．

Answer 1

答案：
解析：

解：(Ⅰ)设动点M的坐标为(x，y)，则＝(x＋1，y)， 　　＝(x－1，y)．由题意·＝． 　　即(x＋1，y)·(x－1，y)＝k[x2＋(y－1)2]． 　　整理，得(1－k)x2＋(1－k)y2＋2ky＝1＋k．即所求动点轨迹方程 　　．当k＝1时，方程化为y＝1，表示过(0，1)点且平行于x轴的直线． 　　．当k≠1时，方程化为x2＋＝，表示以(0，)为圆心，以为半径的圆． 　　(Ⅱ)(文)当k＝2时，方程化为x2＋(y－2)2＝1 　　|＋|＝＝2． 　　＝2＝2 　　∵1≤y≤3　　∴|＋|max＝＝6． 　　|＋|min＝2＝2． 　　(理)当k＝2时，方程化为x2＋(y－2)2＝1． 　　|＋2|＝＝ 　　　　　　　　＝＝ 　　　　　　　　＝． 　　设　　θ∈R， 　　则|＋2|＝＝． 　　其中 　　∴－3＝≤|＋2|≤＝＋3． 　　∴|＋2|max＝＋3．　　∴|＋2|min＝－3．