【题目】在平面直角坐标系
中，圆
的参数方程为
（
为参数），以坐标原点为极点，
轴正半轴为极轴建立极坐标系，直线
的极坐标方程为
.
（1）求圆的普通方程和直线的直角坐标方程；
（2）设
是直线上任意一点，过作圆切线，切点为
，
，求四边形
（点为圆的圆心）面积的最小值.
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案科目：高中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知R为圆
上的一动点，R在x轴，y轴上的射影分别为点S，T，动点P满足
，记动点P的轨迹为曲线C，曲线C与x轴交于A，B两点．
（1）求曲线C的方程；
（2）已知直线AP，BP分别交直线
于点M,N，曲线C在点Р处的切线与线段MN交于点Q，求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点为
，点
在椭圆
上.
（1）设点
到直线
的距离为
，证明：
为定值；
（2）若
是椭圆上的两个动点（都不与重合），直线
的斜率互为相反数，求直线
的斜率（结果用
表示）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在以ABCDEF为顶点的五面体中，底面ABCD为菱形，∠ABC＝120°，AB＝AE＝ED＝2EF，EF
AB，点G为CD中点，平面EAD⊥平面ABCD.
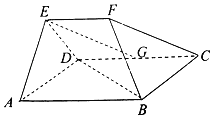
（1）证明：BD⊥EG；
（2）若三棱锥
，求菱形ABCD的边长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市
户居民的月平均用电量（单位：度），以
，
，
，
，
，
，
分组的频率分布直方图如图．
（1）求直方图中
的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取
户居民，则月平均用电量在的用户中应抽取多少户？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求y关于t的线性回归方程；
（2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
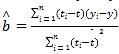查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知在平面直角坐标系中，动点P到定点F(1,0)的距离比到定直线x=-2的距离小1.
（1）求动点P的轨迹C的方程；
（2）若直线l与（1）中轨迹C交于A，B两点，通过A和原点O的直线交直线x=-1于D，求证：直线DB平行于x轴.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某企业引进现代化管理体制，生产效益明显提高。2018年全年总收入与2017年全年总收入相比增长了一倍，实现翻番.同时该企业的各项运营成本也随着收入的变化发生了相应变化。下图给出了该企业这两年不同运营成本占全年总收入的比例，下列说法正确的是（ ）
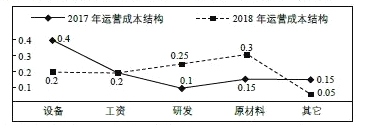
A.该企业2018年设备支出金额是2017年设备支出金额的一半
B.该企业2018年支付工资金额与2017年支付工资金额相当
C.该企业2018年用于研发的费用是2017年用于研发的费用的五倍
D.该企业2018年原材料的费用是2017年原材料的费用的两倍
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
