
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
【答案】
(1)证明:由题意得,an= ![]() =
= ![]() ,
,
又bn+2=3 ![]() an(n∈N*),则bn+2=3
an(n∈N*),则bn+2=3 ![]()
![]() =3n,
=3n,
所以bn=3n﹣2,即bn+1﹣bn=3,且b1=1,
所以{bn}是为1为首项,3为公差的等差数列
(2)证明:解:由(1)得,an= ![]() ,bn=3n﹣2
,bn=3n﹣2
所以cn=anbn= ![]() ,
,
则Sn= ![]() ①,
①,
![]() Sn=
Sn= ![]() ②,
②,
① ﹣②得, ![]() Sn=
Sn= ![]()
![]()
= 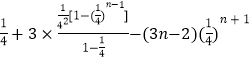
= ![]() ,
,
所以Sn= ![]()
(3)证明:由(2)得,cn= ![]() ,
,
cn+1﹣cn= ![]() ﹣
﹣ ![]() =
= ![]() ,
,
所以当n=1时,c2=c1= ![]() ,
,
当n≥2时,c2=c1>c3>c4>c5>…>cn,
则当n=1或2时,cn的最大值是 ![]() ,
,
因为cn≤ ![]() m2+m﹣1对一切正整数n恒成立,
m2+m﹣1对一切正整数n恒成立,
所以 ![]() ≤
≤ ![]() m2+m﹣1,即m2+4m﹣5≥0,解得m≥1或m≤﹣5,
m2+m﹣1,即m2+4m﹣5≥0,解得m≥1或m≤﹣5,
故实数m的取值范围是m≥1或m≤﹣5
【解析】(1)根据题意和等比数列的通项公式求出an , 再由对数的运算性质求出bn , 根据等差数列的定义进行证明;(2)由(1)和题意求出数列{cn}的通项公式,利用错位相减法能求出数列{cn}的前n项和;(3)先化简cn+1﹣cn , 再根据结果的符号与n的关系,判断出数列{cn}的最大项,将恒成立问题转化为具体的不等式,再求出实数m的取值范围.
【考点精析】根据题目的已知条件,利用数列的前n项和的相关知识可以得到问题的答案,需要掌握数列{an}的前n项和sn与通项an的关系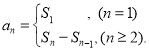 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】种子发芽率与昼夜温差有关.某研究性学习小组对此进行研究,他们分别记录了3月12日至3月16日的昼夜温差与每天100颗某种种子浸泡后的发芽数,如下表:

(I)从3月12日至3月16日中任选2天,记发芽的种子数分别为c,d,求事件“c,d均不小于25”的概率;
(II)请根据3月13日至3月15日的三组数据,求出y关于x的线性回归方程![]() ;
;
(III)若由线性回归方程得到的估计数据与实际数据误差均不超过2颗,则认为回归方程是可靠的,试用3月12日与16日的两组数据检验,(II)中的回归方程是否可靠?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的某中产品中抽取100件,测量这些产品的质量指标值.由测量结果得到如图所示的频率分布直方图,质量指标值落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1. 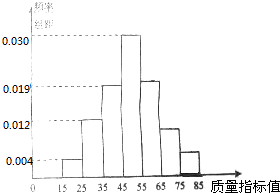
(1)求这些产品质量指标落在区间[75,85]内的概率;
(2)用分层抽样的方法在区间[45,75)内抽取一个容量为6的样本,将该样本看成一个总体,从中任意抽取2件产品,求这2件产品都在区间[45,65)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式a|x|>x2﹣ ![]() 对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
对任意x∈[﹣1,1]都成立,则实数a的取值范围是( )
A.( ![]() ,1)∪(1,+∞)
,1)∪(1,+∞)
B.(0, ![]() )∪(1,+∞)??
)∪(1,+∞)??
C.( ![]() ,1)∪(1,2)
,1)∪(1,2)
D.(0, ![]() )∪(1,2)
)∪(1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图和三视图如图,M是A1B的中点,N是棱B1C1上的任意一点(含顶点). 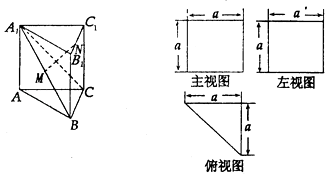
①当点N是棱B1C1的中点时,MN∥平面ACC1A1;
②MN⊥A1C;
③三棱锥N﹣A1BC的体积为VN﹣A ![]() BC=
BC= ![]() a3;
a3;
④点M是该多面体外接球的球心.
其中正确的是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,△PAD与正方形ABCD共用一边AD,平面PAD⊥平面ABCD,其中PA=PD,AB=2,点E是棱PA的中点. 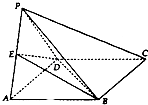
(1)求证:PC∥平面BDE;
(2)若直线PA与平面ABCD所成角为60°,求点A到平面BDE的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是空间两条直线,
是空间两条直线, ![]() 是空间两个平面,则下列命题中不正确的是( )
是空间两个平面,则下列命题中不正确的是( )
A. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
C. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
D. 当![]() 时,“
时,“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知单调递增的等比数列![]() 满足
满足![]() ,且
,且![]() 是
是![]() ,
, ![]() 的等差中项.
的等差中项.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() (
(![]() )是单调递增数列?若存在,求出
)是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com