
【题目】已知中心在原点O,左焦点为F1(-1,0)的椭圆C的左顶点为A,上顶点为B,F1到直线AB的距离为![]() |OB|.
|OB|.
(1)求椭圆C的方程;
(2)如图,若椭圆![]() ,椭圆
,椭圆![]() ,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
,则称椭圆C2是椭圆C1的λ倍相似椭圆.已知C2是椭圆C的3倍相似椭圆,若椭圆C的任意一条切线l交椭圆C2于两点M、N,试求弦长|MN|的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设出椭圆的标准方程,写出直线方程,利用点到直线的距离公式和几何元素间的关系进行求解;(2)先写出相似椭圆的方程,设出直线方程,联立直线和椭圆的方程,得到关于![]() 的一元二次方程,利用根与系数的关系、距离公式进行求解.
的一元二次方程,利用根与系数的关系、距离公式进行求解.
试题解析:(1)设椭圆C的方程为![]() ,
,
∴直线AB的方程为![]() +
+![]() =1.
=1.
∴F1(-1,0)到直线AB距离d=![]() =
=![]() b,
b,
整理得a2+b2=7(a-1)2,
又b2=a2-1,解得a=2,b=![]() ,
,
∴椭圆C的方程为![]() +
+![]() =1.
=1.
(2)椭圆C的3倍相似椭圆C2的方程为![]() +
+![]() =1,
=1,
①若切线l垂直于x轴,则其方程为x=±2,易求得|MN|=2![]() ;
;
②若切线l不垂直于x轴,可设其方程为y=kx+p,
将y=kx+p代入椭圆C的方程,
得(3+4k2)x2+8kpx+4p2-12=0,
∴Δ=(8kp)2-4(3+4k2)(4p2-12)=48(4k2+3-p2)=0,
即p2=4k2+3.(*)
记M、N两点的坐标分别为(x1,y1)、(x2,y2),
将y=kx+p代入椭圆C2的方程,
得(3+4k2)x2+8kpx+4p2-36=0,
此时x1+x2=-![]() ,x1x2=
,x1x2=![]() ,
,
∴|x1-x2|=![]() ,
,
∴|MN|=![]() ·
·![]()
=4![]()
![]() =2
=2![]()
![]() ,
,
∵3+4k2≥3,∴1<1+![]() ≤
≤![]() ,
,
即2![]() <2
<2![]()
![]() ≤4
≤4![]() ,
,
结合①②,得弦长|MN|的取值范围为[2![]() ,4
,4![]() ].
].


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答.统计情况如下表:(单位:人)
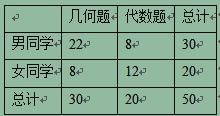
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试发现:女生甲解答一道几何题所用的时间在5—7分钟,女生乙解答一道几何题所用的时间在6—8分钟,现甲、乙两人独立解答同一道几何题,求乙比甲先解答完的概率;
(3)现从选择几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式

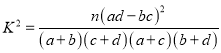
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C: ![]() 的左、右顶点分别为A1、A2,点P在C上且直线PA2的斜率的取值范围是[-2,-1],那么直线PA1斜率的取值范围是________.
的左、右顶点分别为A1、A2,点P在C上且直线PA2的斜率的取值范围是[-2,-1],那么直线PA1斜率的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx和g(x)=m(x2-1)(m∈R).
(1)m=1时,求方程f(x)=g(x)的实根;
(2)若对任意的x∈(1,+∞),函数y=g(x)的图象总在函数y=f(x)图象的上方,求m的取值范围;
(3)求证: ![]() +
+![]() +…+
+…+![]() >ln(2n+1) (n∈N*).
>ln(2n+1) (n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
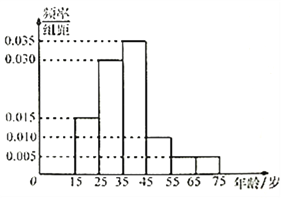
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在![]() 岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为:
岁之间的100人进行调查,并按年龄绘制成频率分布直方图,如图所示,其分组区间为: ![]() ,
, ![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .把年龄落在区间
.把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年”和“中老年”.
内的人分别称为“青少年”和“中老年”.
(1)根据频率分布直方图求样本的中位数(保留两位小数)和众数
(2)根据已知条件完成下面的2×2列联表,并判断能否有99%的把握认为关注“带一路”是否和年龄段有关?
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
附:参考公式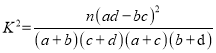 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在2017年五一正式开业,开业期间举行开业大酬宾活动,规定:一次购买总额在区间![]() 内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
内者可以参与一次抽奖,根据统计发现参与一次抽奖的顾客每次购买金额分布情况如下:
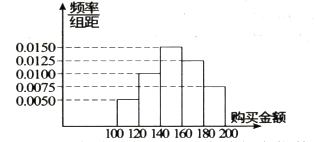
(1)求参与一次抽奖的顾客购买金额的平均数与中位数(同一组中的数据用该组区间的中点值作代表,结果保留到整数);
(2)若根据超市的经营规律,购买金额![]() 与平均利润
与平均利润![]() 有以下四组数据:
有以下四组数据:
![]()
试根据所给数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并根据(1)中计算的结果估计超市对每位顾客所得的利润.
,并根据(1)中计算的结果估计超市对每位顾客所得的利润.
参考公式: 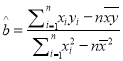 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com