若k进制数123（k）与十进制数38（10）相等，则k= ．
【答案】
分析：不同进制的两个数相等，必须化成同一进制数后才可比较．所以本题的两个不同进制的数，先化成同一进制的数后再进行比较，又因为k进制数123
（k）出现数字3，它至少是4进制数，而k进制数123
（k）与十进制数38
（10）相等，故知k值是唯一确定的，据此，从k=4开始一一代入计算，即可求得答案．
解答：解：由k进制数123可判断k≥4，若k=4，
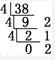
38
（10）=212
（4）不成立．
若k=5，
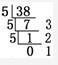
38
（10）=123
（5）成立．
∴k=5．
点评：对于十进制整数转换为k进制的方法，要会换算．
比如：十进制整数转换为二进制整数采用“除2取余，逆序排列“法．具体做法是：用2去除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行，直到商为一时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来．
