
【题目】如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面CDE是等边三角形,棱![]() 。
。

(1)证明FO∥平面CDE;
(2)设BC=![]() CD,证明EO⊥平面CDE。
CD,证明EO⊥平面CDE。
【答案】(1)证明见解析;(2) 证明见解析;
【解析】
(1)利用中点做辅助线,构造出平行四边形即可证明线面平行;(2)根据所给条件构造出菱形,再根据两个对应的线段垂直关系即可得到线面垂直.
证明:(1)取CD中点M,连结OM,连结EM,
在矩形ABCD中,![]() 又
又![]() ,
,
则![]() ,于是四边形EFOM为平行四边形。
,于是四边形EFOM为平行四边形。
∴FO∥EM.
又∵FO![]() 平面CDE,且EM
平面CDE,且EM![]() 平面CDE,
平面CDE,
∴FO∥平面CDE。
(2)连结FM,
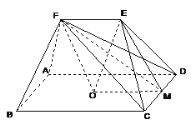
由(1)和已知条件,在等边ΔCDE中,CM=DM,EM⊥CD
且![]()
因此平行四边形EFOM为菱形,从而EO⊥FM.
∵CD⊥OM,CD⊥EM
∴CD⊥平面EOM,
从而CD⊥EO.
而FM![]() CD=M,所以EO⊥平面CDF.
CD=M,所以EO⊥平面CDF.


科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=4cos(ωx﹣ ![]() )sinωx﹣cos(2ωx+π),其中ω>0.
)sinωx﹣cos(2ωx+π),其中ω>0.
(1)求函数y=f(x)的值域
(2)若f(x)在区间 ![]() 上为增函数,求ω的最大值.
上为增函数,求ω的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 满足
满足![]() .当
.当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,则f(1)+f(2)+…+f(2015)=( )
,则f(1)+f(2)+…+f(2015)=( )
A. 333 B. 336 C. 1678 D. 2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为 (t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2
(t为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=2![]() sin θ.
sin θ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A、B,若点P的坐标为(3,![]() ),求|PA|+|PB|.
),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价![]() 元与日销售量
元与日销售量![]() 件之间有如下关系:
件之间有如下关系:
x | 45 | 50 |
y | 27 | 12 |
(1)确定![]() 与
与![]() 的一个一次函数关系式
的一个一次函数关系式![]() ;
;
(2)若日销售利润为P元,根据(I)中关系写出P关于![]() 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是()
A. 锐角是第一象限的角,所以第一象限的角都是锐角;
B. 如果向量![]() ,则
,则![]() ;
;
C. 在![]() 中,记
中,记![]() ,
,![]() ,则向量
,则向量![]() 与
与![]() 可以作为平面ABC内的一组基底;
可以作为平面ABC内的一组基底;
D. 若![]() ,
,![]() 都是单位向量,则
都是单位向量,则![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角坐标系![]() 中,点
中,点![]() 到抛物线
到抛物线![]() 的准线的距离为
的准线的距离为![]() .点
.点![]() 是
是![]() 上的定点,
上的定点,![]() ,
,![]() 是
是![]() 上的两动点,且线段
上的两动点,且线段![]() 的中点
的中点![]() 在直线
在直线![]() 上.
上.
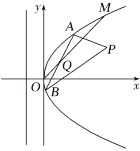
(Ⅰ)求曲线![]() 的方程及
的方程及![]() 的值;
的值;
(Ⅱ)记![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com