
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上异于端点的一点,平面
上异于端点的一点,平面![]()
![]() 平面
平面![]() ,
,![]() .
.

(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析 (Ⅱ)![]()
【解析】
(1)连接AC交BD与O,可证PA//平面BDM,再利用线面平行的性质定理和判定定理即可证得![]() ;
;
(2)根据已知条件建立空间直角坐标系,由线面所成角的正弦值为![]() 可得G的位置,即可求出梯形PAHG的面积,然后可以求四棱锥
可得G的位置,即可求出梯形PAHG的面积,然后可以求四棱锥![]() 的体积.
的体积.
解:(1)证明:连接AC交BD于点O,连接MO.
因为MO是△APC的中位线,所以MO//PA
又PA![]() 平面MBD,MO
平面MBD,MO![]() 平面MBD,所以PA//平面MBD
平面MBD,所以PA//平面MBD
又因为平面GAP∩平面BDM=GH,PA![]() 平面GAP,所以PA//GH
平面GAP,所以PA//GH
又GH![]() 平面PAD,PA
平面PAD,PA![]() 面PAD,所以GH//平面PAD
面PAD,所以GH//平面PAD
(2)如图建立空间直角坐标系.依题意可得D(0,0,0),A(2,0,0),C(0,2,0),P(0,0,2),M(0,1,1)
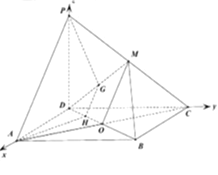
因为G在DM上,所以可设G(0,t,t),(0<t<1)
![]()
设![]() 是平面GAP的一个法向量,则
是平面GAP的一个法向量,则
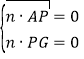 即
即![]() ,
,
可取![]()
若PD与平面GAP所成的角为α,
则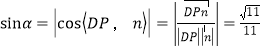
解得![]() ,则G是线段DM的中点
,则G是线段DM的中点
D到平面GAP的距离为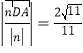
由(1)知MO//PA,PA//GH,所以MO//GH,所以H也是DO的中点,
经计算得![]()
梯形PAHG的高为![]() ,面积为
,面积为![]()
四棱锥D-PAHG的体积![]()


科目:高中数学 来源: 题型:
【题目】![]() 市某机构为了调查该市市民对我国申办
市某机构为了调查该市市民对我国申办![]() 年足球世界杯的态度,随机选取了
年足球世界杯的态度,随机选取了![]() 位市民进行调查,调查结果统计如下:
位市民进行调查,调查结果统计如下:
支持 | 不支持 | 合计 | |
男性市民 |
| ||
女性市民 |
| ||
合计 |
|
|
(1)根据已知数据,把表格数据填写完整;
(2)利用(1)完成的表格数据回答下列问题:
(i)能否在犯错误的概率不超过![]() 的前提下认为支持申办足球世界杯与性别有关;
的前提下认为支持申办足球世界杯与性别有关;
(ii)已知在被调查的支持申办足球世界杯的男性市民中有![]() 位退休老人,其中
位退休老人,其中![]() 位是教师,现从这
位是教师,现从这![]() 位退休老人中随机抽取
位退休老人中随机抽取![]() 人,求至多有
人,求至多有![]() 位老师的概率.
位老师的概率.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为缓解堵车现象,解决堵车问题,银川市交警队调查了甲乙两个路口的车流量,在2019年6月随机选取了14天,统计每天上午7:30-9:00早高峰时段各自的车流量(单位:百辆)得到如图所示的茎叶图,根据茎叶图回答以下问题.

(1)甲乙两个路口的车流量的中位数分别是多少?
(2)试计算甲乙两个路口的车流量在![]() 之间的频率.
之间的频率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统综》中有这样的一个问题:“三百七十八里关,初步健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还”.其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地”,请问此人第2天走的路程为
A. 24里 B. 48里 C. 72里 D. 96里
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发100个红包,每个红包金额为x元,![]() .已知在每轮游戏中所产生的100个红包金额的频率分布直方图如图所示.
.已知在每轮游戏中所产生的100个红包金额的频率分布直方图如图所示.

(1)求a的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在[1,2)的红包个数为X,求X的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+2mx+2lnx,m∈R.
(1)探究函数f(x)的单调性;
(2)若关于x的不等式f(x)≤2![]() +3x2在(0,+∞)上恒成立,求m的取值范围.
+3x2在(0,+∞)上恒成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地草场出现火灾,火势正以每分钟![]() 的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后
的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后![]() 分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火
分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火![]() ,所消耗的灭火材料、劳务津贴等费用为每人每分钟
,所消耗的灭火材料、劳务津贴等费用为每人每分钟![]() 元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为30元.
元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为30元.
(1)设派![]() 名消防队员前去救火,用
名消防队员前去救火,用![]() 分钟将火扑灭,试建立
分钟将火扑灭,试建立![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)问应该派多少消防队员前去救火,才能使总损失最少?(注:总损失费=灭火劳务津贴+车辆、器械装备费+森林损失费)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com