
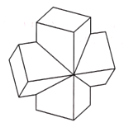
【题目】下图是某机械零件的几何结构,该几何体是由两个相同的直四棱柱组合而成的,且前后,左右、上下均对称,每个四棱柱的底面都是边长为2的正方形,高为4,且两个四棱柱的侧棱互相垂直.则这个几何体的体积为________.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,过点
,过点![]() 的直线
的直线![]()
![]() 与
与![]() 相交于
相交于![]() 两点,点
两点,点![]() 为线段
为线段![]() 的中点.
的中点.
(1)当![]() 的倾斜角为
的倾斜角为![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(2)试探究在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
设函数f(x)=x+ax2+blnx,曲线y=f(x)过P(1,0),且在P点处的切斜线率为2.
(I)求a,b的值;
(II)证明:f(x)≤2x-2。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满400元的顾客,将获得一次摸奖机会,规则如下:奖盒中放有除颜色外完全相同的1个红球,1个黄球,1个白球和1个黑球顾客不放回的每次摸出1个球,若摸到黑球则停止摸奖,否则就继续摸球规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励
(1)求1名顾客摸球2次停止摸奖的概率:
(2)记![]() 为1名顾客5次摸奖获得的奖金数额,求随机变量
为1名顾客5次摸奖获得的奖金数额,求随机变量![]() 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是坐标原点,过
是坐标原点,过![]() 的直线分别交抛物线
的直线分别交抛物线![]() 于
于![]() 、
、![]() 两点,直线
两点,直线![]() 与过点
与过点![]() 平行于
平行于![]() 轴的直线相交于点
轴的直线相交于点![]() ,过点
,过点![]() 与此抛物线相切的直线与直线
与此抛物线相切的直线与直线![]() 相交于点
相交于点![]() .则
.则![]() ( )
( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]() 的焦点,过F的动直线交抛物线C于A,B两点.当直线与x轴垂直时,
的焦点,过F的动直线交抛物线C于A,B两点.当直线与x轴垂直时,![]() .
.
(1)求抛物线C的方程;
(2)若直线AB与抛物线的准线l相交于点M,在抛物线C上是否存在点P,使得直线PA,PM,PB的斜率成等差数列?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com