
【题目】在平面直角坐标系中,有两个圆![]() 和
和![]() ,其中
,其中![]() ,
,![]() 为正常数,满足
为正常数,满足![]() 或
或![]() ,一个动圆
,一个动圆![]() 与两圆都相切,则动圆圆心的轨迹方程可以是( )
与两圆都相切,则动圆圆心的轨迹方程可以是( )
A.两个椭圆B.两个双曲线
C.一个双曲线和一条直线D.一个椭圆和一个双曲线
【答案】BCD
【解析】
根据题意可知当![]() ,即两圆外离时, 当
,即两圆外离时, 当![]() ,两圆相交,再分情况讨论动圆这两个圆相切的类型求轨迹即可.
,两圆相交,再分情况讨论动圆这两个圆相切的类型求轨迹即可.
根据题意圆![]() ,半径
,半径![]() ,圆
,圆![]() ,半径
,半径![]() ,所以
,所以![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,
,
(1)当![]() ,即两圆外离时,动圆
,即两圆外离时,动圆![]() 可能与两圆均内切或均外切或一个内切一个外切,
可能与两圆均内切或均外切或一个内切一个外切,
①均内切时![]() ,
,![]() ,此时
,此时![]() ,
,
当![]() 时,此时
时,此时![]() 点的轨迹是以
点的轨迹是以![]() ,
,![]() 为焦点的双曲线,
为焦点的双曲线,
当![]() 时,此时点
时,此时点![]() 在
在![]() ,
,![]() 的垂直平分线上.
的垂直平分线上.
②均外切时![]() ,
,![]() ,此时
,此时![]() ,此时
,此时![]() 点的轨迹是与①相同.
点的轨迹是与①相同.
③与一个内切与一个外切时,不妨设与圆![]() 内切,与圆
内切,与圆![]() 外切,
外切,
![]() ,
,![]() ,
,![]()
与圆![]() 内切,与圆
内切,与圆![]() 外切时,同理得,
外切时,同理得,![]()
此时点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的双曲线,与①中双曲线不一样.
为焦点的双曲线,与①中双曲线不一样.
(2)当![]() ,两圆相交,动圆
,两圆相交,动圆![]() 可能与两圆均内切或均外切或一个内切一个外切,
可能与两圆均内切或均外切或一个内切一个外切,
④均内切时轨迹和①相同.
⑤均外切时轨迹和①相同
⑥与一个内切另一个外切时,不妨设与圆![]() 内切,与圆
内切,与圆![]() 外切,
外切,
![]() ,
,![]() ,
,![]() ,此时点
,此时点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆.
为焦点的椭圆.
与圆![]() 内切,与圆
内切,与圆![]() 外切时,同理得
外切时,同理得![]() ,
,
此时点![]() 的轨迹是以
的轨迹是以![]() ,
,![]() 为焦点的椭圆.
为焦点的椭圆.
故选:BCD


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:

附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:


(1)求高二(1)班全体女生的人数;
(2)由频率分布直方图估计该班女生此次数学测试成绩的众数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】画糖是一种以糖为材料在石板上进行造型的民间艺术,常见于公园与旅游景点.某师傅制作了一种新造型糖画,为了进行合理定价先进性试销售,其单价![]() (元)与销量
(元)与销量![]() (个)相关数据如下表:
(个)相关数据如下表:

(1)已知销量![]() 与单价
与单价![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性相关方程;
的线性相关方程;
(2)若该新造型糖画每个的成本为![]() 元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
元,要使得进入售卖时利润最大,请利用所求的线性相关关系确定单价应该定为多少元?(结果保留到整数)
参考公式:线性回归方程![]() 中斜率和截距最小二乘法估计计算公式:
中斜率和截距最小二乘法估计计算公式:

![]() .参考数据:
.参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,且抛物线的准线被椭圆
的焦点重合,且抛物线的准线被椭圆![]() 截得的弦长为1,
截得的弦长为1,![]() 是直线
是直线![]() 上一点,过点
上一点,过点![]() 且与
且与![]() 垂直的直线交椭圆于
垂直的直线交椭圆于![]() 两点.
两点.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() 的斜率分别为
的斜率分别为![]() ,求证:
,求证:![]() 成等差数列.
成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点为别为F1、F2,且过点
的左、右焦点为别为F1、F2,且过点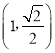 和
和 .
.

(1)求椭圆的标准方程;
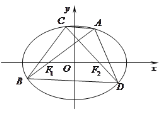
(2)如图,点A为椭圆上一位于x轴上方的动点,AF2的延长线与椭圆交于点B,AO的延长线与椭圆交于点C,求△ABC面积的最大值,并写出取到最大值时直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且点
,且点![]() 和
和![]() 分别为
分别为![]() 和
和![]() 的中点
的中点

(I)求证:![]() 平面
平面![]() ;
;
(II)求二面角![]() 的正弦值;
的正弦值;
(III)设![]() 为棱
为棱![]() 上的点,若直线
上的点,若直线![]() 和平面
和平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长。
的长。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且经过点P
,且经过点P![]() ,过它的左、右焦点
,过它的左、右焦点![]() 分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且
分别作直线l1和12.l1交椭圆于A.两点,l2交椭圆于C,D两点, 且![]()
(1)求椭圆的标准方程.
(2)求四边形ACBD的面积S的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com