
分析 (1)求出圆心和半径.设过该点的直线方程,求圆心到直线的距离与半径和半弦长构成勾股定理,解出斜率k,即得到直线方程,注意讨论斜率不存在的情况;
(2)求出直线方程,圆心坐标与半径,从而可得圆上的点到直线距离的最小值,进而可求△ABC的面积最小值.
解答 解:(1)圆C:x2+y2+4x-12y+24=0,其圆心坐标为(-2,6),半径为r=4,点P(0,5),
当直线斜率不存在时,直线方程为:x=0,
当x=0时,y2-12y+24=0,解得y=6±2$\sqrt{3}$,
可得弦长为6+2$\sqrt{3}$-(6-2$\sqrt{3}$)=4$\sqrt{3}$成立;
当直线斜率存在时,设过P的直线方程为:y=kx+5,化为一般方程:kx-y+5=0,
圆心到直线的距离d=$\frac{|-2k-6+5|}{\sqrt{1+{k}^{2}}}$=$\frac{|2k+1|}{\sqrt{1+{k}^{2}}}$.
又(2$\sqrt{3}$)2+d2=r2=16,
解得:k=$\frac{3}{4}$,
所以3x-4y+20=0,
综上可得直线l:x=0或3x-4y+20=0;
(2)直线MN的方程为-x+y=1,即x-y+1=0.
圆C:x2+y2+4x-12y+24=0,其圆心坐标为(-2,6),半径为r=4,
可得圆心(-2,6)到直线MN的距离为d=$\frac{|-2-6+1|}{\sqrt{2}}$=$\frac{7\sqrt{2}}{2}$,
圆上的点到直线距离的最小值为$\frac{7\sqrt{2}}{2}$-4.
由|MN|=$\sqrt{2}$,可得△ABC的面积最小值是$\frac{1}{2}$×$\sqrt{2}$×($\frac{7\sqrt{2}}{2}$-4)=$\frac{7}{2}$-2$\sqrt{2}$.
点评 本题考查求直线的方程,注意运用点到直线的距离公式、弦长公式,考查三角形的面积的最小值,注意运用转化思想,求得圆上点到直线的最小值,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
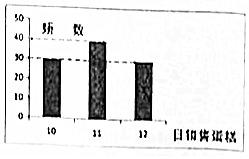 某超市每两天购入一批某型号的生日蛋糕进行销售,进价50元/个,售价60元/个,若每次购入的生日蛋糕两天内没有售完,则以40元/个的价格可以全部处理掉,根据此超市以往随机抽取的100天此类蛋糕的销售情况,如柱形图所示.设n为每次购入的蛋糕数,ξ为两天内的蛋糕销售数量,W为此批购入的蛋糕销售的利润(视频率为概率,且每天销售情况是独立的)
某超市每两天购入一批某型号的生日蛋糕进行销售,进价50元/个,售价60元/个,若每次购入的生日蛋糕两天内没有售完,则以40元/个的价格可以全部处理掉,根据此超市以往随机抽取的100天此类蛋糕的销售情况,如柱形图所示.设n为每次购入的蛋糕数,ξ为两天内的蛋糕销售数量,W为此批购入的蛋糕销售的利润(视频率为概率,且每天销售情况是独立的)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-1=0 | B. | x+y-1=0 | C. | x-y+1=0 | D. | x+y+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{12}$ | C. | $\frac{7\sqrt{3}}{12}$ | D. | -$\frac{7\sqrt{3}}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com