已知x=4是函数f(x)=alnx+x2-12x+11的一个极值点.
(1)求实数a的值;
(2)求函数f(x)的单调区间;
(3)若直线y=b与函数y=f(x)的图象有3个交点,求b的取值范围.
【答案】
分析:(1)求导函数,利用x=4是函数f(x)=alnx+x
2-12x+11的一个极值点,可得f′(4)=0,从而可求a的值;
(2)利用导数的正负,可得函数f(x)的单调区间;
(3)确定函数的极值,从而可得不等式,即可求b的取值范围.
解答:解:(1)求导函数可得f′(x)=
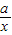
+2x-12,
∵x=4是函数f(x)=alnx+x
2-12x+11的一个极值点
∴f′(4)=
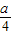
+8-12=0,∴a=16 …3分
(2)由(1)知,f(x)=16lnx+x
2-12x+11,x∈(0,+∞)
f′(x)=
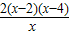
…5分
当x∈(0,2)∪(4,+∞)时,f′(x)>0;当x∈(2,4)时,f′(x)<0…7分
所以f(x)的单调增区间是(0,2),(4,+∞),f(x)的单凋减区间是(2,4)…8分
(3)由(2)知,f(x)的极大值为f(2)=16ln2-9,极小值为f(4)=32ln2-21
因此f(16)=16ln16+16
2-12×16+11>16ln2-9=f(2),f(e
-2)<-32+11=-21<f(4)
所以在f(x)的三个单调区间(0,2),(2,4),(4,+∞)内,直线y=b与y=f(x)的图象各有一个交点,
当且仅当f(4)<b<f(2)成立…13分
因此,b的取值范围为(32ln2-21,16ln2-9). …14分.
点评:本题考查导数知识的运用,考查函数的极值,考查函数的单调性,考查学生的计算能力,正确求导是关键.

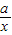 +2x-12,
+2x-12,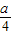 +8-12=0,∴a=16 …3分
+8-12=0,∴a=16 …3分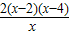 …5分
…5分

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案