
【题目】从某企业生产的产品中抽取1000件测量这些产品的一项质量指标值,由测量结果得到频率分布直方图如图所示.
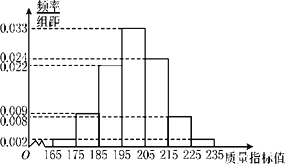
(Ⅰ)求这1000件产品质量指标值的样本平均数![]() 和样本方差s2(同一组数据用该区间的中点值作代表).
和样本方差s2(同一组数据用该区间的中点值作代表).
(Ⅱ)由频率分布直方图可以认为这种产品的质量指标值Z服从正态分布N(μ,δ2),其中μ近似为样本平均数![]() ,δ2近似为样本方差s2.
,δ2近似为样本方差s2.
![]() 利用该正态分布,求P(175.6<Z<224.4);
利用该正态分布,求P(175.6<Z<224.4);
②某用户从该企业购买了100件这种产品,估计其中质量指标值位于区间(175.6,224.4)的产品件数.(精确到个位)
附: ![]() ≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
P(μ-2δ<Z<μ+2δ)=0.9544
【答案】(Ⅰ)![]() ;(Ⅱ)①0.9544,②95件.
;(Ⅱ)①0.9544,②95件.
【解析】试题分析:(Ⅰ)运用离散型随机变量的期望和方差公式,即可求出;
(Ⅱ)①由(1)知![]() ,从而求出
,从而求出![]() ,即可得出结论;
,即可得出结论;
②由①知,一件产品的质量指标值位于区间(175.6,224.4)的概率为0.9544即可估算..
试题解析:
(Ⅰ)
![]() =170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
=170×0.02+180×0.09+190×0.22+200×0.33+210×0.24+220×0.08+230×0.02=200,
s2=(-30)2×0.02+(-20)2×0.09+(-10)2×0.22+0×0.33+102×0.24+202×0.08+302×0.02=150.
(Ⅱ)①由(Ⅰ)知,Z~N(200,150),从而
P(175.6<Z<224.4)=P(200-2×12.2<Z<200+2×12.2)=0.9544.
②由①知,一件产品的质量指标值位于区间(175.6,224.4)的概率为0.9544, 用户从该企业购买了100件这种产品中质量指标值位于区间(175.6,224.4)的产品件数为100×0.9544 ![]() 95 (件)
95 (件)


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点为
的左焦点为![]() ,其左、右顶点为
,其左、右顶点为![]() 、
、![]() ,椭圆与
,椭圆与![]() 轴正半轴的交点为
轴正半轴的交点为![]() ,
,![]() 的外接圆的圆心
的外接圆的圆心![]() 在直线
在直线![]() 上.
上.
(I)求椭圆![]() 的方程;
的方程;
(II)已知直线![]() :
:![]() ,
,![]() 是椭圆
是椭圆![]() 上的动点,
上的动点,![]() ,垂足为
,垂足为![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,求出点
为等腰三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: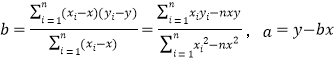 ,).
,).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)为定义在R上的奇函数.如图是函数图象的一部分,当0≤x≤2时,是线段OA;当x>2时,图象是顶点为P(3,4)的抛物线的一部分.
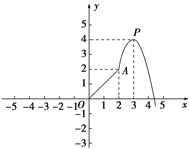
(1)在图中的直角坐标系中画出函数f(x)的图象;
(2)求函数f(x)在[2,+∞)上的解析式;
(3)写出函数f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在颈椎病患者越来越多,甚至大学生也出现了颈椎病,年轻人患颈椎病多与工作、生活方式有关,某调查机构为了了解大学生患有颈椎病是否与长期过度使用电子产品有关,在遂宁市中心医院随机的对入院的50名大学生进行了问卷调查,得到了如下的4×4列联表:
未过度使用 | 过度使用 | 合计 | |
未患颈椎病 | 15 | 5 | 20 |
患颈椎病 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)是否有99.5%的把握认为大学生患颈锥病与长期过度使用电子产品有关?
(2)已知在患有颈锥病的10名未过度使用电子产品的大学生中,有3名大学生又患有肠胃炎,现在从上述的10名大学生中,抽取3名大学生进行其他方面的排查,记选出患肠胃炎的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据与公式:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() ,且
,且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .试比较
.试比较![]() 与0的关系,并给出理由.
与0的关系,并给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度x的一次函数.
是车流密度x的一次函数.
①当![]() 时,求函数
时,求函数![]() 的表达式.
的表达式.
②当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com