
【题目】如图,斜三棱柱ABC﹣A1B1C1的侧面AA1C1C是菱形,侧面ABB1A1⊥侧面AA1C1C,A1B=AB=AA1=2,△AA1C1的面积为 ![]() ,且∠AA1C1为锐角.
,且∠AA1C1为锐角.
(I) 求证:AA1⊥BC1;
(Ⅱ)求锐二面角B﹣AC﹣C1的余弦值.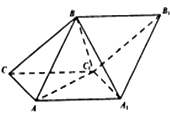
【答案】证明:(Ⅰ)∵侧面AA1C1C是菱形,且A1B=AB=AA1=2,
∴AA1=A1C1=C1C=CD=2,△AA1B是等边三角形,
取AA1的中点D,连结DB、DC1 , 则AA1⊥BD,
由 ![]() =
= ![]() =2sin∠AA1C1=
=2sin∠AA1C1= ![]() ,
,
得sin∠AA1C1= ![]() ,
,
又∠AA1C1为锐角,
∴∠AA1C1=60°,
∴△AA1C1是等边三角形,且AA1⊥C1D,
又∵BD平面BC1D,C1D平面BC1D,BD∩C1D=D,
∴AA1⊥平面BC1D,
∴AA1⊥BC1 .
解:(Ⅱ)由(Ⅰ)知AA1⊥BD,
又∵侧面ABB1A1⊥侧面AA1C1C,
侧面ABB1A1∩侧面AA1C1C=AA1 , BD平面ABB1A1 ,
∴BD⊥平面AA1C1C,
以D为原点,C1D为x轴,DA1为y轴,DB为z轴,建立空间直角坐标系,
则A(0,﹣1,0),A1(0,1,0),C1(﹣ ![]() ,0,0),B(0,0,
,0,0),B(0,0, ![]() ),D(0,0,0),
),D(0,0,0),![]() ,
, ![]() =(0,1,
=(0,1, ![]() ),
),![]() =(0,0,
=(0,0, ![]() )是平面ACC1的一个法向量,
)是平面ACC1的一个法向量,
设 ![]() =(x,y,z)是平面ABC的一个法向量,
=(x,y,z)是平面ABC的一个法向量,
则  ,令z=1,得
,令z=1,得 ![]() =(1,﹣
=(1,﹣ ![]() ,1),
,1),
∴cos< ![]() >=
>=  =
= ![]() =
= ![]() ,
,
∴锐二面角B﹣AC﹣C1的余弦值为 ![]() .
.

【解析】(Ⅰ)推导出△AA1B是等边三角形,取AA1的中点D,则AA1⊥BD,再推导出△AA1C1是等边三角形,且AA1⊥C1D,由此能证明AA1⊥BC1 . (Ⅱ)以D为原点,C1D为x轴,DA1为y轴,DB为z轴,建立空间直角坐标系,利用向量法能求出锐二面角B﹣AC﹣C1的余弦值.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】如图所示,A是函数f(x)=2x的图象上的动点,过点A作直线平行于x轴,交函数g(x)=2x+2的图象于点B,若函数f(x)=2x的图象上存在点C使得△ABC为等边三角形,则称A为函数f(x)=2x上的好位置点.函数f(x)=2x上的好位置点的个数为( ) 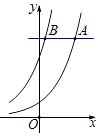
A.0
B.1
C.2
D.大于2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,倾斜角为
,倾斜角为![]() 的直线与椭圆相交于
的直线与椭圆相交于![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() .过椭圆
.过椭圆![]() 内一点
内一点![]() 的两条直线分别与椭圆交于点
的两条直线分别与椭圆交于点![]() ,且满足
,且满足![]() ,其中
,其中![]() 为实数.当直线
为实数.当直线![]() 平行于
平行于![]() 轴时,对应的
轴时,对应的![]() .
.
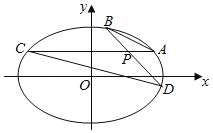
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当![]() 变化时,
变化时,![]() 是否为定值?若是,请求出此定值;若不是,请说明理由.
是否为定值?若是,请求出此定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三一班举办消防安全知识竞赛,分别选出3名男生和3名女生组成男队和女队,每人一道必答题,答对则为本队得10分,答错与不答都得0分,已知男队每人答对的概率依次为 ![]() ,
, ![]() ,
, ![]() ,女队每人答对的概率都是
,女队每人答对的概率都是 ![]() ,设每人回答正确与否相互之间没有影响,用X表示男队的总得分.
,设每人回答正确与否相互之间没有影响,用X表示男队的总得分.
(I) 求X的分布列及其数学期望E(X);
(Ⅱ)求在男队和女队得分之和为50的条件下,男队比女队得分高的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)= ![]() (a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
(a>0,且a≠1)的值域为(﹣∞,+∞),则实数a的取值范围是( )
A.(3,+∞)
B.(0, ![]() ]
]
C.(1,3)
D.[ ![]() ,1)
,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且3cosAcosB+1=3sinAsinB+cos2C.
(1)求∠C
(2)若△ABC的面积为5 ![]() ,b=5,求sinA.
,b=5,求sinA.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且3cosAcosB+1=3sinAsinB+cos2C.
(1)求∠C
(2)若△ABC的面积为5 ![]() ,b=5,求sinA.
,b=5,求sinA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com