
分析 (1)利用两角和的正弦函数以及二倍角公式化简求解即可.
(2)利用平方关系式化简已知条件,化简所求的表达式,代入求解即可.
解答 解:(1)$\frac{1}{{sin{{10}°}}}-\frac{{\sqrt{3}}}{{sin{{80}°}}}=\frac{1}{{sin{{10}°}}}-\frac{{\sqrt{3}}}{{cos{{10}°}}}$…(1分)
=$\frac{{cos{{10}°}-\sqrt{3}sin{{10}°}}}{{sin{{10}°}cos{{10}°}}}$…(2分)
=$\frac{{2(-\frac{{\sqrt{3}}}{2}{{sin}°}+\frac{1}{2}cos{{10}°})}}{{sin{{10}°}cos{{10}°}}}$…(3分)
=$\frac{{2sin({{150}°}+{{10}°})}}{{sin{{10}°}cos{{10}°}}}$…(4分)
=$\frac{{2sin{{160}°}}}{{\frac{1}{2}sin{{20}°}}}=\frac{{2sin{{20}°}}}{{\frac{1}{2}sin{{20}°}}}$…(5分)
=4…(6分)
(2)由$sinx+cosx=\frac{1}{5}$,两边平方得:$2sinxcosx=-\frac{24}{25}$…(7分)
所以${(sinx-cosx)^2}=1-2sinxcosx=\frac{49}{25}$…(8分)
因为$-\frac{π}{2}<x<0$,所以sinx<0,cosx>0
故$sinx-cos=-\frac{7}{5}$…(9分)
所以$\frac{{sin2x+2{{sin}^2}x}}{1-tanx}=\frac{2sinx(cosx+sinx)}{{1-\frac{sinx}{cosx}}}=\frac{2sinxcosx(cosx+sinx)}{cosx-sinx}$…(11分)
=$\frac{{-\frac{24}{25}×\frac{1}{5}}}{{\frac{7}{5}}}=-\frac{24}{175}$…(12分)
点评 本题考查三角函数的化简求值,二倍角公式以及两角和与差的三角函数的应用,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
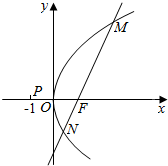 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,3} | B. | {1,4,5} | C. | {1,4,5,6} | D. | {1,2,3,4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com