
【题目】命题正确的是( )
A.若一个平面内由无穷多个点到另一个平面的距离相等,则这两个平面平行;
B.一个平面内的两条相交直线与另一个平面内的两条相交直线分别垂直,则这两个平面垂直;
C.若一个平面内有3条两两不平行的直线与另一个平面所成角均相等,则这两个平面平行;
D.若两个平面相交,则一个平面内不存在不共线三点到另一个平面距离相等.
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的长轴长为4.
的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是椭圆
是椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 是该椭圆上一点,若当
是该椭圆上一点,若当![]() 时,
时,![]() 面积达到最大,最大值为
面积达到最大,最大值为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() 为坐标原点,是否存在过左焦点
为坐标原点,是否存在过左焦点![]() 的直线
的直线![]() ,与椭圆交于
,与椭圆交于![]() 两点,使得
两点,使得![]() 的面积为
的面积为![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年双十一落下帷幕,天猫交易额定格在268(单位:十亿元)人民币(下同),再创新高,比去年218(十亿元)多了50(十亿元),这些数字的背后,除了是消费者买买买的表现,更是购物车里中国新消费的奇迹,为了研究历年销售额的变化趋势,一机构统计了2010年到2019年天猫双十一的销售额数据![]() (单位:十亿元),绘制如下表1:
(单位:十亿元),绘制如下表1:
表1
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
销售额 | 0.9 | 8.7 | 22.4 | 41 | 65 | 94 | 132.5 | 172.5 | 218 | 268 |
根据以上数据绘制散点图,如图所示.

(1)把销售额超过100(十亿元)的年份叫“畅销年”,把销售额超过200(十亿元)的年份叫“狂欢年”,从2010年到2019年这十年的“畅销年”中任取2个,求至少取到一个“狂欢年”的概率;
(2)根据散点图判断,![]() 与
与![]() 哪一个适宜作为销售额
哪一个适宜作为销售额![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(3)根据(2)的判断结果及下表中的数据,建立![]() 关于
关于![]() 的回归方程,并预测2020年天猫双十一的销售额.(注:数据保留小数点后一位)
的回归方程,并预测2020年天猫双十一的销售额.(注:数据保留小数点后一位)
参考数据:![]() ,
,
|
|
|
|
|
|
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为
的斜率和截距的最小二乘估计公式分别为 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() 的底面是边长为
的底面是边长为![]() 的菱形,
的菱形,![]() ,点E是棱BC的中点,
,点E是棱BC的中点,![]() ,点P在平面ABCD的射影为O,F为棱PA上一点.
,点P在平面ABCD的射影为O,F为棱PA上一点.
![]() 1
1![]() 求证:平面
求证:平面![]() 平面BCF;
平面BCF;
![]() 2
2![]() 若
若![]() 平面PDE,
平面PDE,![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的准线方程为x=﹣1.
(1)求抛物线C的方程;
(2)过抛物线C的焦点作直线l,交抛物线C于A,B两点,若线段AB中点的横坐标为6,求|AB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少儿游泳队需对队员进行限时的仰卧起坐达标测试.已知队员的测试分数![]() 与仰卧起坐
与仰卧起坐
个数![]() 之间的关系如下:
之间的关系如下: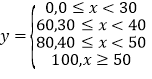 ;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
;测试规则:每位队员最多进行三组测试,每组限时1分钟,当一组测完,测试成绩达到60分或以上时,就以此组测试成绩作为该队员的成绩,无需再进行后续的测试,最多进行三组;根据以往的训练统计,队员“喵儿”在一分钟内限时测试的频率分布直方图如下:
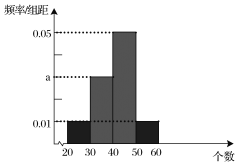
(1)计算![]() 值;
值;
(2)以此样本的频率作为概率,求
①在本次达标测试中,“喵儿”得分等于![]() 的概率;
的概率;
②“喵儿”在本次达标测试中可能得分的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com