
【题目】某市居民自来水收费标准如下:每户每月用水不超过4吨时,每吨为![]() 元,当用水超过4吨时,超过部分每吨为
元,当用水超过4吨时,超过部分每吨为![]() 元,每月甲、乙两户共交水费
元,每月甲、乙两户共交水费![]() 元,已知甲、乙两户该月用水量分别为
元,已知甲、乙两户该月用水量分别为![]() .
.
(1)求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)若甲、乙两户该月共交水费![]() 元,分别求出甲、乙两户该月的用水量.
元,分别求出甲、乙两户该月的用水量.
【答案】(1)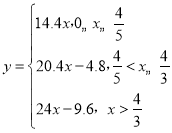 ;(2)甲户用水量为7.5吨,乙户用水量为4.5吨
;(2)甲户用水量为7.5吨,乙户用水量为4.5吨
【解析】
(1)由题意知:x≥0,令5x=4,得x=![]() ;令3x=4,得x=
;令3x=4,得x=![]() .将x取值范围分三段,求对应函数解析式可得答案.
.将x取值范围分三段,求对应函数解析式可得答案.
(2)在分段函数各定义域上讨论函数值对应的x的值.
(1)由题意知,x≥0,令5x=4,得x=![]() ;令3x=4,得x=
;令3x=4,得x=![]() .
.
则当0≤x≤![]() 时,
时,
y=(5x+3x)×1.8=14.4x,
当![]() <x≤
<x≤![]() 时,
时,
y=4×1.8+(x![]() )×5×3+3x1.8=20.4x4.8,
)×5×3+3x1.8=20.4x4.8,
当x>![]() 时,y=(4+4)×1.8+(
时,y=(4+4)×1.8+(![]()
![]() )×5×3+3×5(x
)×5×3+3×5(x![]() )+3×3(x
)+3×3(x![]() )=24x9.6,
)=24x9.6,
即得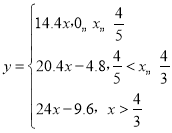 ;
;
(2)由于y=f(x)在各段区间上均单增,
当0≤x≤![]() 时,y≤f(
时,y≤f(![]() )<26.4,
)<26.4,
当![]() <x≤
<x≤![]() 时,y≤f(
时,y≤f(![]() )<26.4,
)<26.4,
当x>![]() 时,令24x9.6=26.4,得x=1.5,
时,令24x9.6=26.4,得x=1.5,
所以甲户用水量为5x=7.5吨,付费S1=4×1.8+3.5×3=17.70元
乙户用水量为3x=4.5吨,付费S2=8.7元.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】中国有个名句“运筹帷幄之中,决胜千里之外”.其中的“筹”原意是指《孙 子算经》中记载的算筹,古代是用算筹来进行计算,算筹是将几寸长的小竹棍摆在平面上进行运算,算筹的摆放形式有纵横两种形式,如下表:
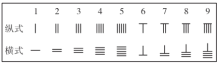
表示一个多位数时,像阿拉伯计数一样,把各个数位的数码从左到右排 列,但各位数码的筹式需要纵横相间,个位,百位,万位用纵式表示,十位,千位,十万位用横式表示,以此类推,例如2268用算筹表示就是=||丄|||.执行如图所示程序框 图,若输人的x=1, y = 2,则输出的S用算筹表示为![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面PAC⊥平面ABC,![]() 是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,
是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,![]() .
.

(1)设G是OC的中点,证明:![]() ∥平面
∥平面![]() ;
;
(2)证明:在![]() 内存在一点M,使FM⊥平面BOE,求点M到OA,OB的距离.
内存在一点M,使FM⊥平面BOE,求点M到OA,OB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 底面的3个顶点
底面的3个顶点![]() 在球
在球![]() 的同一个大圆上,且
的同一个大圆上,且![]() 为正三角形,
为正三角形,![]() 为该球面上的点,若三棱锥
为该球面上的点,若三棱锥![]() 体积的最大值为
体积的最大值为![]() ,则球
,则球![]() 的表面积为( )
的表面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年10月中上旬是小麦的最佳种植时间,但小麦的发芽会受到土壤、气候等多方面因素的影响.某科技小组为了解昼夜温差的大小与小麦发芽的多少之间的关系,在不同的温差下统计了100颗小麦种子的发芽数,得到了如下数据:
温差 | 8 | 10 | 11 | 12 | 13 |
发芽数 | 79 | 81 | 85 | 86 | 90 |
(1)请根据统计的最后三组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由(1)中的线性回归方程得到的估计值与前两组数据的实际值误差均不超过两颗,则认为线性回归方程是可靠的,试判断(1)中得到的线性回归方程是否可靠;
(3)若100颗小麦种子的发芽率为![]() 颗,则记为
颗,则记为![]() 的发芽率,当发芽率为
的发芽率,当发芽率为![]() 时,平均每亩地的收益为
时,平均每亩地的收益为![]() 元,某农场有土地10万亩,小麦种植期间昼夜温差大约为
元,某农场有土地10万亩,小麦种植期间昼夜温差大约为![]() ,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
,根据(1)中得到的线性回归方程估计该农场种植小麦所获得的收益.
附:在线性回归方程![]() 中,
中,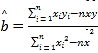 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() ,求
,求![]() 的最大值及此时直线
的最大值及此时直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱![]() 各条棱的长度均相等,
各条棱的长度均相等,![]() 为
为![]() 的中点,
的中点,![]() 分别是线段
分别是线段![]() 和线段
和线段![]() 的动点(含端点),且满足
的动点(含端点),且满足![]() ,当
,当![]() 运动时,下列结论中不正确的是
运动时,下列结论中不正确的是

A. 在![]() 内总存在与平面
内总存在与平面![]() 平行的线段
平行的线段
B. 平面![]() 平面
平面![]()
C. 三棱锥![]() 的体积为定值
的体积为定值
D. ![]() 可能为直角三角形
可能为直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com