
分析 根据抛物线的解析式y2=2px(p>0),写出抛物线的焦点、对称轴以及准线,然后根据通径|AB|=2p,求出p,△ABP的面积是|AB|与DP乘积一半.
解答 解:由于抛物线的解析式为y2=2px(p>0),
则焦点为F($\frac{p}{2}$,0),对称轴为x轴,准线为x=-$\frac{p}{2}$,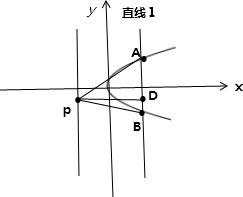
∵直线l经过抛物线的焦点,A、B是l与C的交点,
又∵AB⊥x轴
∴|AB|=2p=10
∴p=5
又∵点P在准线上
∴DP=$\frac{p}{2}$+|-$\frac{p}{2}$|=p=5
∴S△ABP=$\frac{1}{2}$DP•AB=$\frac{1}{2}$×5×10=25
故答案为25.
点评 本题主要考查抛物线焦点、对称轴、准线以及焦点弦的特点;关于直线和圆锥曲线的关系问题一般采取数形结合法.


科目:高中数学 来源: 题型:解答题
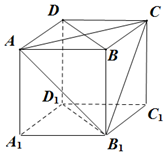 如图,在正方体ABCD-A1B1C1D1 中,
如图,在正方体ABCD-A1B1C1D1 中,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 81 | D. | $\frac{81}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,40] | B. | [160,+∞) | C. | [40,160] | D. | (-∞,40]∪[160,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-$\frac{\sqrt{3}π}{6}$ | B. | 1-$\frac{\sqrt{3}π}{12}$ | C. | 1-$\frac{\sqrt{3}π}{9}$ | D. | 1-$\frac{\sqrt{3}π}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
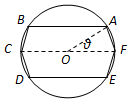 某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.
某休闲广场中央有一个半径为1(百米)的圆形花坛,现计划在该花坛内建造一条六边形观光步道,围出一个由两个全等的等腰梯形(梯形ABCF和梯形DEFC)构成的六边形ABCDEF区域,其中A、B、C、D、E、F都在圆周上,CF为圆的直径(如图).设∠AOF=θ,其中O为圆心.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com