
ЁОЬтФПЁПФГЪаашЖдФГЛЗГЧПьЫйГЕЕРНјааЯоЫйЃЌЮЊСЫЕїбаИУЕРТЗГЕЫйЧщПіЃЌгкФГИіЪБЖЮЫцЛњЖд ![]() СОГЕЕФЫйЖШНјааШЁбљЃЌВтСПЕФГЕЫйжЦГЩШчЯТЬѕаЮЭМЃК
СОГЕЕФЫйЖШНјааШЁбљЃЌВтСПЕФГЕЫйжЦГЩШчЯТЬѕаЮЭМЃК
ОМЦЫуЃКбљБОЕФЦНОљжЕ ![]() ЃЌБъзМВю
ЃЌБъзМВю ![]() ЃЌвдЦЕТЪжЕзїЮЊИХТЪЕФЙРМЦжЕ.вбжЊГЕЫйЙ§Т§гыЙ§ПьЖМБЛШЯЮЊЪЧашНУе§ЫйЖШЃЌЯжЙцЖЈГЕЫйаЁгк
ЃЌвдЦЕТЪжЕзїЮЊИХТЪЕФЙРМЦжЕ.вбжЊГЕЫйЙ§Т§гыЙ§ПьЖМБЛШЯЮЊЪЧашНУе§ЫйЖШЃЌЯжЙцЖЈГЕЫйаЁгк ![]() ЛђГЕЫйДѓгк
ЛђГЕЫйДѓгк ![]() ЪЧашНУе§ЫйЖШ.
ЪЧашНУе§ЫйЖШ.
ЃЈ1ЃЉДгИУПьЫйГЕЕРЩЯЫљгаГЕСОжаШЮШЁ ![]() ИіЃЌЧѓИУГЕСОЪЧашНУе§ЫйЖШЕФИХТЪЃЛ
ИіЃЌЧѓИУГЕСОЪЧашНУе§ЫйЖШЕФИХТЪЃЛ
ЃЈ2ЃЉ ДгбљБОжаШЮШЁ
ДгбљБОжаШЮШЁ ![]() ИіГЕСОЃЌЧѓет
ИіГЕСОЃЌЧѓет ![]() ИіГЕСООљЪЧашНУе§ЫйЖШЕФИХТЪ
ИіГЕСООљЪЧашНУе§ЫйЖШЕФИХТЪ
ЃЈ3ЃЉДгИУПьЫйГЕЕРЩЯЫљгаГЕСОжаШЮШЁ ![]() ИіЃЌМЧЦфжаЪЧашНУе§ЫйЖШЕФИіЪ§ЮЊ
ИіЃЌМЧЦфжаЪЧашНУе§ЫйЖШЕФИіЪ§ЮЊ ![]() ЃЌЧѓ
ЃЌЧѓ ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЕФЗжВМСаКЭЪ§бЇЦкЭћ.
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКМЧЪТМў ![]() ЮЊЁАДгИУПьЫйГЕЕРЩЯЫљгаГЕСОжаШЮШЁ
ЮЊЁАДгИУПьЫйГЕЕРЩЯЫљгаГЕСОжаШЮШЁ ![]() ИіЃЌИУГЕСОЪЧашНУе§ЫйЖШЁБЃЌ
ИіЃЌИУГЕСОЪЧашНУе§ЫйЖШЁБЃЌ
вђЮЊ ![]() ЃЌ
ЃЌ
гЩбљБОЬѕаЮЭМПЩжЊЃЌЫљЧѓЕФИХТЪЮЊP(A)=![]()
ЃЈ2ЃЉНтЃКМЧЪТМў ![]() ЮЊЁАДгбљБОжаШЮШЁ
ЮЊЁАДгбљБОжаШЮШЁ ![]() ИіГЕСОЃЌет
ИіГЕСОЃЌет ![]() ИіГЕСООљЪЧашНУе§ЫйЖШЁБ
ИіГЕСООљЪЧашНУе§ЫйЖШЁБ
гЩЬтЩшПЩжЊбљБОШнСПЮЊ ![]() ЃЌгжашНУе§ЫйЖШИіЪ§ЮЊ
ЃЌгжашНУе§ЫйЖШИіЪ§ЮЊ ![]() ИіЃЌЙЪЫљЧѓИХТЪЮЊ
ИіЃЌЙЪЫљЧѓИХТЪЮЊ ![]()
ЃЈ3ЃЉНтЃКашНУе§ЫйЖШЕФИіЪ§ ![]() ЗўДгЖўЯюЗжВМЃЌМД
ЗўДгЖўЯюЗжВМЃЌМД ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
вђДЫ ![]() ЕФЗжВМСаЮЊ
ЕФЗжВМСаЮЊ
|
|
|
|
|
|
|
|
гЩ ![]() ЃЌжЊЪ§бЇЦкЭћ
ЃЌжЊЪ§бЇЦкЭћ ![]()
ЁОНтЮіЁП(1)ИљОнЬтвтгЩвбжЊПЩЕУГі ІЬ 3 Ів = 78.4 , ІЬ + 2 Ів = 89.4ЃЌЙлВьбљБОЬѕаЮЭМгЩЭМПЩжЊP(A)=![]() ЧѓГіЦфжЕМДПЩЁЃ(2)РћгУвбжЊгЩЬтЩшПЩжЊбљБОШнСПЮЊ100ЃЌгжашНУе§ЫйЖШИіЪ§ЮЊ 5 ИіИљОнИХТЪЕФЖЈвхЧѓГіБШжЕЁЃ(3)АДееЖўЯюЗжВМЕФЙЋЪН
ЧѓГіЦфжЕМДПЩЁЃ(2)РћгУвбжЊгЩЬтЩшПЩжЊбљБОШнСПЮЊ100ЃЌгжашНУе§ЫйЖШИіЪ§ЮЊ 5 ИіИљОнИХТЪЕФЖЈвхЧѓГіБШжЕЁЃ(3)АДееЖўЯюЗжВМЕФЙЋЪН![]() ж№вЛДњШыЪ§жЕМЦЫуГіНсЙћСаБэМДПЩЃЌдйНсКЯЪ§бЇЦкЭћ
ж№вЛДњШыЪ§жЕМЦЫуГіНсЙћСаБэМДПЩЃЌдйНсКЯЪ§бЇЦкЭћ![]() ЕФЙЋЪНДњШыЪ§жЕЧѓГіМДПЩЁЃ
ЕФЙЋЪНДњШыЪ§жЕЧѓГіМДПЩЁЃ
ЁОПМЕуОЋЮіЁПЭЈЙ§СщЛюдЫгУгУбљБОЕФЦЕТЪЗжВМЙРМЦзмЬхЗжВМЃЌеЦЮебљБОЪ§ОнЕФЦЕТЪЗжВМБэКЭЦЕТЪЗжВМжБЗНЭМЃЌЪЧЭЈЙ§ИїаЁзщЪ§ОндкбљБОШнСПжаЫљеМБШР§ДѓаЁРДБэЪОЪ§ОнЕФЗжВМЙцТЩЃЌЫќПЩвдШУЮвУЧИќЧхГўЕФПДЕНећИібљБОЪ§ОнЕФЦЕТЪЗжВМЧщПіЃЌВЂгЩДЫЙРМЦзмЬхЕФЗжВМЧщПіМДПЩвдНтД№ДЫЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФЖрУцЬхжаЃЌEFЁЭЦНУцAEBЃЌAEЁЭEBЃЌADЁЮEFЃЌEFЁЮBCЃЌBC=2AD=4ЃЌEF=3ЃЌAE=BE=2ЃЌGЪЧBCЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКBDЁЭEGЃЛ
ЃЈ2ЃЉЧѓЦНУцDEGгыЦНУцDEFЫљГЩШёЖўУцНЧЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхдкЃЈ0ЃЌ+ЁоЃЉЩЯЕФКЏЪ§y=fЃЈxЃЉЕФЗДКЏЪ§ЮЊy=fЉ1ЃЈxЃЉЃЌШєgЃЈxЃЉ= ![]() ЮЊЦцКЏЪ§ЃЌдђfЉ1ЃЈxЃЉ=2ЕФНтЮЊ ЃЎ
ЮЊЦцКЏЪ§ЃЌдђfЉ1ЃЈxЃЉ=2ЕФНтЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧКЏЪ§ ![]() ЭМЯѓЕФвЛВПЗжЃЎЮЊСЫЕУЕНетИіКЏЪ§ЕФЭМЯѓЃЌжЛвЊНЋy=sinx(xЁЪR)ЕФЭМЯѓЩЯЫљгаЕФЕуЃЈ ЃЉ
ЭМЯѓЕФвЛВПЗжЃЎЮЊСЫЕУЕНетИіКЏЪ§ЕФЭМЯѓЃЌжЛвЊНЋy=sinx(xЁЪR)ЕФЭМЯѓЩЯЫљгаЕФЕуЃЈ ЃЉ
A.ЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ ![]() ЃЌзнзјБъВЛБф
ЃЌзнзјБъВЛБф
B.ЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф
C.ЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ ![]() ЃЌзнзјБъВЛБф
ЃЌзнзјБъВЛБф
D.ЯђзѓЦНвЦ ![]() ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф
ИіЕЅЮЛГЄЖШЃЌдйАбЫљЕУИїЕуЕФКсзјБъЩьГЄЕНдРДЕФ2БЖЃЌзнзјБъВЛБф
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќЦкЁАЙВЯэЕЅГЕЁБдкШЋЙњЖрИіГЧЪаГжајЩ§ЮТЃЌФГвЦЖЏЛЅСЊЭјЛњЙЙЭЈЙ§ЖдЪЙгУепЕФЕїВщЕУГіЃЌЯждкЪаГЁЩЯГЃМћЕФАЫИіЦЗХЦЕФЁАЙВЯэЕЅГЕЁБЕФТњвтЖШжИЪ§ШчОЅвЖЭМЫљЪОЃК
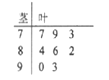
ЃЈЂёЃЉЧѓГіетзщЪ§ОнЕФЦНОљЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂђЃЉФГгУЛЇДгТњвтЖШжИЪ§ГЌЙ§80ЕФЦЗХЦжаЫцЛњбЁдёСНИіЦЗХЦЪЙгУЃЌЧѓЫљбЁСНИіЦЗХЦЕФТњвтЖШжИЪ§ОљГЌЙ§85ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЧјМф[0ЃЌ1]ФкЫцЛњШЁСНИіЪ§ЗжБ№ЮЊaЃЌbЃЌдђЪЙЕУЗНГЬx2+2ax+b2=0гаЪЕИљЕФИХТЪЮЊЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋдВ ![]() ЮЊВЮЪ§ЃЉЩЯЕФУПвЛЕуЕФКсзјБъБЃГжВЛБфЃЌзнзјБъБфЮЊдРДЕФ
ЮЊВЮЪ§ЃЉЩЯЕФУПвЛЕуЕФКсзјБъБЃГжВЛБфЃЌзнзјБъБфЮЊдРДЕФ ![]() БЖЃЌЕУЕНЧњЯпCЃЎ
БЖЃЌЕУЕНЧњЯпCЃЎ
ЃЈ1ЃЉЧѓГіCЕФЦеЭЈЗНГЬЃЛ
ЃЈ2ЃЉЩшжБЯпlЃКx+2yЉ2=0гыCЕФНЛЕуЮЊP1 ЃЌ P2 ЃЌ вдзјБъдЕуЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌ ЧѓЙ§ЯпЖЮP1P2ЕФжаЕуЧвгыlДЙжБЕФжБЯпЕФМЋзјБъЗНГЬЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшfЃЈxЃЉЪЧЖЈвхдкRЩЯжмЦкЮЊ2ЕФЦцКЏЪ§ЃЌЕБ0ЁмxЁм1ЪБЃЌfЃЈxЃЉ=x2ЉxЃЌдђ ![]() =ЃЈ ЃЉ
=ЃЈ ЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіаЁЧђДг100УзИпДІздгЩТфЯТЃЌУПДЮзХЕиКѓгжЬјЛиЕНдИпЖШЕФвЛАыдйТфЯТЃЎжДааЯТУцЕФГЬађПђЭМЃЌдђЪфГіЕФSБэЪОЕФЪЧЃЈ ЃЉ 
A.аЁЧђЕк10ДЮзХЕиЪБЯђЯТЕФдЫЖЏЙВОЙ§ЕФТЗГЬ
B.аЁЧђЕк11ДЮзХЕиЪБЯђЯТЕФдЫЖЏЙВОЙ§ЕФТЗГЬ
C.аЁЧђЕк10ДЮзХЕиЪБвЛЙВОЙ§ЕФТЗГЬ
D.аЁЧђЕк11ДЮзХЕиЪБвЛЙВОЙ§ЕФТЗГЬ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com