
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的零点;
的零点;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)当![]() 时,若
时,若![]() 对
对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)当
;(Ⅱ)当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)由![]() ,可知当
,可知当![]() 时,
时,![]() ,
,
可得两零点分别为![]()
![]() 和
和![]()
![]() ;(Ⅱ)由
;(Ⅱ)由![]() ,得
,得![]() 或
或![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况进行讨论;(Ⅲ)由
三种情况进行讨论;(Ⅲ)由![]() 求得函数
求得函数![]() 在
在![]() 上的最小值
上的最小值![]() ,若不等式
,若不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() ,解得
,解得![]() .
.
试题解析:(Ⅰ)令![]() ,即
,即![]() 。
。
因为![]() ,所以
,所以![]() 。
。
![]() ,因为
,因为![]() ,所以
,所以![]() 。
。
所以方程![]() 有两个不等实根:
有两个不等实根:![]() 。
。
所以函数![]() 有且只有两个零点
有且只有两个零点![]()
![]() 和
和![]()
![]() 。
。
(Ⅱ)![]() 。
。
令![]() ,即
,即![]() ,解得
,解得![]() 或
或![]() 。
。
当![]() ,列表得:
,列表得:
|
|
|
| 1 |
|
|
| 0 |
| 0 |
|
| 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
当![]() 时,
时,
(1)若![]() ,则
,则![]() ,列表得
,列表得
|
|
|
| 1 |
|
|
| 0 |
| 0 |
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
(2)若![]() ,则
,则![]() ,列表得
,列表得
|
| 1 |
|
|
|
|
| 0 |
| 0 |
|
| 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
综上,当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() ;
;
当![]() 时,
时,![]() 单调递增区间为
单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]() 。
。
(Ⅲ)因为![]() ,所以当
,所以当![]() 时,有
时,有![]() ,
,
所以![]() ,从而
,从而![]() 。
。
当![]() 时,由(Ⅱ)可知函数在
时,由(Ⅱ)可知函数在![]() 时取得最小值
时取得最小值![]() 。
。
所以![]() 为函数
为函数![]() 在
在![]() 上的最小值。
上的最小值。
由题意,不等式![]() 对
对![]() 恒成立,
恒成立,
所以得![]() ,解得
,解得![]() 。
。
所以![]() 的取值范围是
的取值范围是![]() 。
。


科目:高中数学 来源: 题型:
【题目】中秋节到了,糕点店的售货员很忙,请设计一个程序,帮助售货员算账,已知豆沙馅的月饼每千克25元,蛋黄馅的月饼每千克35元,莲蓉馅的月饼每千克30元,那么依次购买这三种月饼a、b、c千克,应收多少钱?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]()
上是单调函数;②![]() 在
在 ![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数 ![]() 的“和谐区间”,
的“和谐区间”,
下列结论错误的是( )
A.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
B.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
C.函数 ![]() 不存在 “和谐区间”
不存在 “和谐区间”
D.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出对程序框图的几种说法:
①任何一个程序框图都必须有起止框;②输入框只能紧接开始框,输出框只能紧接结束框;③判断框是唯一具有超出一个退出点的符号;④对于一个问题的算法来说,其程序框图判断框内的条件的表述方法是唯一的.
其中正确说法的个数是__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.“x>5”是“x>3”的必要不充分条件
B.命题“对x∈R,恒有x2+1>0”的否定是“x∈R,使得x2+1≤0”
C.m∈R,使函数f(x)=x2+mx(x∈R)是奇函数
D.设p,q是简单命题,若p∨q是真命题,则p∧q也是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第组
人参加“学雷锋”志愿活动,按年龄分组:第组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有人年龄在第
人参加社区宣传交流活动,求至少有人年龄在第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是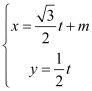 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com