练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    将边长为的等边三角形沿轴滚动，某时刻与坐标原点重合（如图），设顶点的轨迹方程是，关于函数的有下列说法：

    ①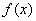的值域为；

    ②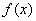是周期函数；

    ③；

    ④.

    其中正确的说法个数为:

    A．0                B．1                C．               D．

     

    【答案】

    C

    【解析】

    试题分析：由题意，画出函数的图形，如图所示：所以函数的值域为，是周期函数，周期为4，，，

    又易知函数在上单调递减，所以，即

    ，又易知，所以②④正确.选C.

    考点：函数的性质

    点评：本题借助具体函数实例考查函数的性质，关键是准确的做出函数的图形，借助图形分

    析函数的性质.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年上海市嘉定区高三上学期期末考试（一模）理科数学试卷（解析版） 题型：填空题

    某种平面分形图如下图所示，一级分形图是一个边长为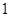的等边三角形（图（1））；二级分形图是将一级分形图的每条线段三等分，并以中间的那一条线段为一底边向形外作等边三角形，然后去掉底边（图（2））；将二级分形图的每条线段三等边，重复上述的作图方法，得到三级分形图（图（3））；…；重复上述作图方法，依次得到四级、五级、…、级分形图．则级分形图的周长为__________．

     

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广东省高三高考预测数学试卷（解析版） 题型：解答题

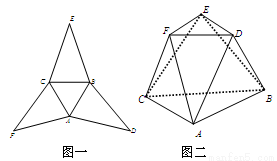
    在图一所示的平面图形中，是边长为 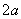的等边三角形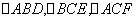，是分别以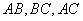为底的全等的等腰三角形，现将该平面图形分别沿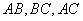折叠，使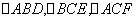所在平面都与平面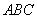垂直，连接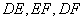,得到图二所示的几何体，据此几何体解决下面问题.

    （1）求证：;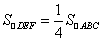

    （2）当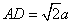时，求三棱锥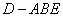的体积；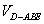

    （3）在（2）的前提下，求二面角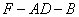的余弦值.

     

    查看答案和解析>>

    科目：高中数学 来源：2012-2013年浙江台州六校高二上期中联考理科数学试卷（解析版） 题型：选择题

    将边长为的正方形沿对角线折起，使得平面平面，在折起后形成的三棱锥中，给出下列三个命题：

    ①面是等边三角形；  ②；  ③三棱锥的体积是.

    其中正确命题的个数为(    )

    A．0               B．1             C．2              D．3

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年巢湖市质检二） 边长为的等边三角形内任一点到三边距离之和为定值，这个定值等于_____；将这个结论推广到空间是：棱长为的正四面体内任一点到各面距离之和等于       .

    查看答案和解析>>

    同步练习册答案