【题目】过正方体ABCD﹣A1B1C1D1的顶点A1在空间作直线l，使l与直线AC和BC1所成的角都等于 
，则这样的直线l共可以作出（ ）
A.1条
B.2条
C.3条
D.4条
【答案】C
【解析】解：因为AD1∥BC1，所以直线AC和BC1所成的角即为直线AC和AD1所成的角，所以过A1在空间作直线l，使l与直线AC和BC1所成的角都等于 
，即过点A在空间作直线l，使l与直线AC和AD1所成的角都等于 ．
因为∠ACD1=60°，∠ACD1的外角平分线与AC和AD1所成的角相等，均为60°，所以在平面ACD1内有一条满足要求．
因为∠ACD1的角平分线与AC和AD1所成的角相等，均为30°，将角平分线绕点A向上转动到与面ACD1垂直的过程中，存在两条直线与直线AC和BC1所成的角都等于 ，故符合条件的直线有3条．
故选C
【考点精析】关于本题考查的空间中直线与直线之间的位置关系，需要了解相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能得出正确答案．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】如图，在四棱锥E﹣ABCD中，底面ABCD为正方形，AE⊥平面CDE，已知AE=DE=2，F为线段DF的中点． （I）求证：BE∥平面ACF；
（II）求平面BCF与平面BEF所成锐二面角的余弦角．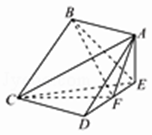
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
已知直线l过定点P（1，1），且倾斜角为 
，以坐标原点为极点，x轴的正半轴为极轴的坐标系中，曲线C的极坐标方程为 
．
（1）求曲线C的直角坐标方程与直线l的参数方程；
（2）若直线l与曲线C相交于不同的两点A，B，求|AB|及|PA||PB|的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】平面上，点A、C为射线PM上的两点，点B、D为射线PN上的两点，则有 
（其中S△PAB、S△PCD分别为△PAB、△PCD的面积）；空间中，点A、C为射线PM上的两点，点B、D为射线PN上的两点，点E、F为射线PL上的两点，则有 
=（其中VP﹣ABE、VP﹣CDF分别为四面体P﹣ABE、P﹣CDF的体积）． 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】由于雾霾日趋严重，政府号召市民乘公交出行．但公交车的数量太多会造成资源的浪费，太少又难以满足乘客需求．为此，某市公交公司在某站台的60名候车乘客中进行随机抽样，共抽取10人进行调查反馈，所选乘客情况如下表所示：
组别 | 候车时间（单位：min） | 人数 |
一 | [0，5） | 1 |
二 | [5，10） | 5 |
三 | [10，15） | 3 |
四 | [15，20） | 1 |
（1）估计这60名乘客中候车时间少于10分钟的人数；
（2）现从这10人中随机取3人，求至少有一人来自第二组的概率；
（3）现从这10人中随机抽取3人进行问卷调查，设这3个人共来自X个组，求X的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】渝州集团对所有员工进行了职业技能测试从甲、乙两部门中各任选10名员工的测试成绩（单位：分）数据的茎叶图如图所示． 
（1）若公司决定测试成绩高于85分的员工获得“职业技能好能手”称号，求从这20名员工中任选三人，其中恰有两人获得“职业技能好能手”的概率；
（2）公司结合这次测试成绩对员工的绩效奖金进行调整（绩效奖金方案如表），若以甲部门这10人的样本数据来估计该部门总体数据，且以频率估计概率，从甲部门所有员工中任选3名员工，记绩效奖金不小于3a的人数为ξ，求ξ的分布列及数学期望．
分数 | [60，70） | [70，80） | [80，90） | [90，100] |
奖金 | a | 2a | 3a | 4a |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=sin（ωx+ 
）（x∈R，ω＞0）的最小正周期为π，将y=f（x）的图象向左平移|φ|个单位长度，所得函数y=f（x）为偶函数时，则φ的一个值是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】袋中有6个编号不同的黑球和3个编号不同的白球，这9个球的大小及质地都相同，现从该袋中随机摸取3个球，则这三个球中恰有两个黑球和一个白球的方法总数是 ， 设摸取的这三个球中所含的黑球数为X，则P（X=k）取最大值时，k的值为 ．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
