
【题目】已知椭圆C:![]() 1(a>b>0)的一个顶点坐标为A(0,﹣1),离心率为
1(a>b>0)的一个顶点坐标为A(0,﹣1),离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线y=k(x﹣1)(k![]() 0)与椭圆C交于不同的两点P,Q,线段PQ的中点为M,点B(1,0),求证:点M不在以AB为直径的圆上.
0)与椭圆C交于不同的两点P,Q,线段PQ的中点为M,点B(1,0),求证:点M不在以AB为直径的圆上.
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】
(Ⅰ)由已知列出关于![]() 的方程组可解得结论;
的方程组可解得结论;
(Ⅱ)设P(x1,y1),Q(x2,y2),M(x0,y0),由直线方程与椭圆方程联立消去![]() 后整理,应用韦达定理得
后整理,应用韦达定理得![]() ,求出中点
,求出中点![]() 坐标,计算
坐标,计算![]() ,证明
,证明![]() 即可,
即可,
(Ⅰ)解:由题意可知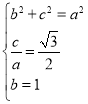
解得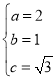
所以椭圆C的方程为![]() .
.
(Ⅱ)证明:设P(x1,y1),Q(x2,y2),M(x0,y0),.
由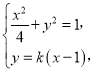 得(4k2+1)x2﹣8k2x+4k2﹣4=0,
得(4k2+1)x2﹣8k2x+4k2﹣4=0,
所以△=(﹣8k2)2﹣4×(4k2+1)(4k2﹣4)=48k2+16.
所以当k为任何实数时,都有△>0.
所以 ![]() ,
,![]() .
.
因为线段PQ的中点为M,
所以 ![]() ,
,![]() ,
,
因为 B(1,0),
所以 ![]() ,
,![]() .
.
所以 ![]()
![]()

 .
.
又因为 k![]() 0,
0,![]() ,
,
所以 ![]() ,
,
所以点M不在以AB为直径的圆上.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是数列1,
是数列1,![]() ,
,![]() ,…,
,…,![]() 的各项和,
的各项和,![]() ,
,![]() .
.
(1)设![]() ,证明:
,证明:![]() 在
在![]() 内有且只有一个零点;
内有且只有一个零点;
(2)当![]() 时,设存在一个与上述数列的首项、项数、末项都相同的等差数列,其各项和为
时,设存在一个与上述数列的首项、项数、末项都相同的等差数列,其各项和为![]() ,比较
,比较![]() 与
与![]() 的大小,并说明理由;
的大小,并说明理由;
(3)给出由公式![]() 推导出公式
推导出公式![]() 的一种方法如下:在公式
的一种方法如下:在公式![]() 中两边求导得:
中两边求导得:![]() ,所以
,所以![]() 成立,请类比该方法,利用上述数列的末项
成立,请类比该方法,利用上述数列的末项![]() 的二项展开式证明:
的二项展开式证明:![]() 时
时![]() (其中
(其中![]() 表示组合数)
表示组合数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F的直线与抛物线交于A,B两点,点O为坐标原点,则下列命题中正确的个数为( )
的焦点为F,过F的直线与抛物线交于A,B两点,点O为坐标原点,则下列命题中正确的个数为( )
①![]() 面积的最小值为4;
面积的最小值为4;
②以![]() 为直径的圆与x轴相切;
为直径的圆与x轴相切;
③记![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,则
,则![]() ;
;
④过焦点F作y轴的垂线与直线![]() ,
,![]() 分别交于点M,N,则以
分别交于点M,N,则以![]() 为直径的圆恒过定点.
为直径的圆恒过定点.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 是定义域为
是定义域为![]() 的奇函数,且它的最小正周期是T,已知
的奇函数,且它的最小正周期是T,已知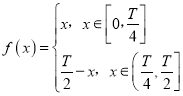 ,
,![]() .给出下列四个判断:①对于给定的正整数
.给出下列四个判断:①对于给定的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 成立;②当a
成立;②当a![]() 时,对于给定的正整数
时,对于给定的正整数![]() ,存在
,存在![]() ,使得
,使得![]() 成立;③当
成立;③当![]()
![]() 时,函数
时,函数![]() 既有对称轴又有对称中心;④当
既有对称轴又有对称中心;④当![]()
![]() 时,
时,![]() 的值只有0或
的值只有0或![]() .其中正确判断的有( )
.其中正确判断的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]()
![]() 的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495;命题
的展开式中,仅有第7项的二项式系数最大,则展开式中的常数项为495;命题![]() 随机变量
随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .现给出四个命题:①
.现给出四个命题:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() ,其中真命题的是( )
,其中真命题的是( )
A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣sinx+ax(a>0).
(1)若a=1,求证:当x∈(1,![]() )时,f(x)<2x﹣1;
)时,f(x)<2x﹣1;
(2)若f(x)在(0,2π)上有且仅有1个极值点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在《周髀算经》中,把圆及其内接正方形称为圆方图,把正方形及其内切圆称为方圆图.圆方图和方圆图在我国古代的设计和建筑领域有着广泛的应用.山西应县木塔是我国现存最古老、最高大的纯木结构楼阁式建筑,它的正面图如图所示.以该木塔底层的边![]() 作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点
作方形,会发现塔的高度正好跟此对角线长度相等.以塔底座的边作方形.作方圆图,会发现方圆的切点![]() 正好位于塔身和塔顶的分界.经测量发现,木塔底层的边
正好位于塔身和塔顶的分界.经测量发现,木塔底层的边![]() 不少于
不少于![]() 米,塔顶
米,塔顶![]() 到点
到点![]() 的距离不超过
的距离不超过![]() 米,则该木塔的高度可能是(参考数据:
米,则该木塔的高度可能是(参考数据:![]() )( )
)( )

A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中![]() 中,曲线C的参数方程
中,曲线C的参数方程![]() (
(![]() 为参数,
为参数,![]() ).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线
).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设P是曲线C上的一个动点,当![]() 时,求点P到直线
时,求点P到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线C上所有的点均在直线![]() 的右下方,求t的取值范围.
的右下方,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com