
【题目】已知函数![]() 是定义在实数集
是定义在实数集![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]()
![]() ,若集合
,若集合![]() ,则实数
,则实数![]() 的取值范围是______.
的取值范围是______.
【答案】![]()
【解析】
把x≥0时的f(x)改写成分段函数,求出其最小值,由函数的奇偶性可得x<0时的函数的最大值,条件等价为对x∈R,都有f(x-1)![]() f(x),进行转化求解即可求解该不等式得答案.
f(x),进行转化求解即可求解该不等式得答案.
若![]() =,
=,
则等价为f(x-1)-f(x)![]() 0恒成立,即f(x-1)
0恒成立,即f(x-1)![]() f(x)恒成立,
f(x)恒成立,
当x≥0时![]()
![]() .
.
若a≤0,
则当x≥0时,![]() ,
,
∵f(x)是奇函数,
∴若x<0,则-x>0,则f(-x)=-x=-f(x),
则f(x)=x,x<0,
综上f(x)=x,此时函数为增函数,则f(x-1)![]() f(x)恒成立;
f(x)恒成立;
若a>0,
若0≤x≤a时,![]() ;
;
当a<x≤2a时,![]() ;
;
当x>2a时,![]() .即当x≥0时,函数的最小值为-a,
.即当x≥0时,函数的最小值为-a,
由于函数f(x)是定义在R上的奇函数,
当x<0时,f(x)的最大值为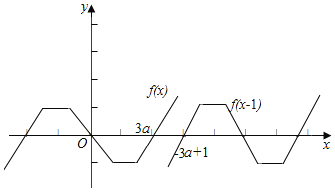 a,
a,
作出函数的图象如图:
由于x∈R,f(x-1)![]() f(x),
f(x),
故函数f(x-1)的图象不能在函数f(x)的图象的上方,
结合图可得![]() ,即6a
,即6a![]() 2,求得0<a
2,求得0<a![]()
![]() ,
,
综上a![]()
![]() ,
,
故答案为:![]()


科目:高中数学 来源: 题型:
【题目】在约束条件 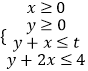 下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
下,当t≥0时,其所表示的平面区域的面积为S(t),S(t)与t之间的函数关系用下列图象表示,正确的应该是( )
A.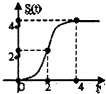
B.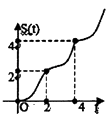
C.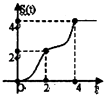
D.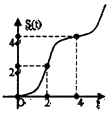
查看答案和解析>>
科目:高中数学 来源: 题型:
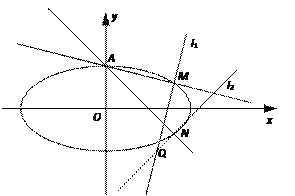
【题目】在平面直角坐标系xOy中,已知椭圆C: ![]() (a>b>0)的一条准线方程为x=
(a>b>0)的一条准线方程为x=![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆C的方程;
(2)如图,设A为椭圆的上顶点,过点A作两条直线AM,AN,分别与椭圆C相交于M,N两点,且直线MN垂直于x轴.
① 设直线AM,AN的斜率分别是k1, k2,求k1k2的值;
② 过M作直线l1⊥AM,过N作直线l2⊥AN,l1与l2相交于点Q.试问:点Q是否在一条定直线上?若在,求出该直线的方程;若不在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业一天中不同时刻的用电量![]() (万千瓦时)关于时间
(万千瓦时)关于时间![]() (小时,
(小时,![]() )的函数
)的函数![]() 近似满足
近似满足![]() ,如图是函数
,如图是函数![]() 的部分图象(
的部分图象(![]() 对应凌晨
对应凌晨![]() 点).
点).

(Ⅰ)根据图象,求![]() 的值;
的值;
(Ⅱ)由于当地冬季雾霾严重,从环保的角度,既要控制火力发电厂的排放量,电力供应有限;又要控制企业的排放量,于是需要对各企业实行分时拉闸限电措施.已知该企业某日前半日能分配到的供电量![]() (万千瓦时)与时间
(万千瓦时)与时间![]() (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型![]() 模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
模拟.当供电量小于该企业的用电量时,企业就必须停产.初步预计停产时间在中午11点到12点间,为保证该企业既可提前准备应对停产,又可尽量减少停产时间,请从这个初步预计的时间段开始,用二分法帮其估算出精确到15分钟的停产时间段.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,且anan+1=2n , n∈N* , 则数列{an}的通项公式为( )
A.an=( ![]() )n﹣1
)n﹣1
B.an=( ![]() )n
)n
C.an= ![]()
D.an= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}中,已知a1=2,a4=16.
(1)求数列{an}的通项公式an;
(2)若a3 , a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com