
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
: ![]() 的离心率是
的离心率是![]() ,且直线
,且直线![]() :
: ![]() 被椭圆
被椭圆![]() 截得的弦长为
截得的弦长为![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若直线![]() 与圆
与圆![]() :
: ![]() 相切:
相切:
(i)求圆![]() 的标准方程;
的标准方程;
(ii)若直线![]() 过定点
过定点![]() ,与椭圆
,与椭圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,与圆
,与圆![]() 交于不同的两点
交于不同的两点![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(I)![]() ;(II)(i)
;(II)(i)![]() ;(ii)
;(ii)![]() .
.
【解析】试题分析:(Ⅰ)由直线![]() 过定点
过定点![]() ,
, ![]() ,可得到
,可得到![]() ,再结合
,再结合![]() ,即可求出椭圆的方程;(Ⅱ)(i)利用圆的几何性质,求出圆心到直线
,即可求出椭圆的方程;(Ⅱ)(i)利用圆的几何性质,求出圆心到直线![]() 的距离等于半径,即可求出
的距离等于半径,即可求出![]() 的值,即可求出圆
的值,即可求出圆![]() 的标准方程;(ii)首先设直线
的标准方程;(ii)首先设直线![]() 的方程为
的方程为![]() ,利用韦达定理即可求出弦长
,利用韦达定理即可求出弦长![]() 的表达式,同理利用圆的几何关系可求出弦长
的表达式,同理利用圆的几何关系可求出弦长![]() 的表达式,即可得到
的表达式,即可得到![]() 的表达式,再用换元法
的表达式,再用换元法![]() ,即可求出
,即可求出![]() 的取值范围.
的取值范围.
试题解析:
解:(Ⅰ)由已知得直线![]() 过定点
过定点![]() ,
, ![]() ,
, ![]() ,
,
又![]() ,
, ![]() ,解得
,解得![]() ,
, ![]() ,
,
故所求椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(i)由(Ⅰ)得直线![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
又圆![]() 的标准方程为
的标准方程为![]() ,
,
∴圆心为![]() ,圆的半径
,圆的半径![]() ,
,
∴圆![]() 的标准方程为
的标准方程为![]() .
.
(ii)由题可得直线![]() 的斜率存在,
的斜率存在,
设![]() :
: ![]() ,与椭圆
,与椭圆![]() 的两个交点为
的两个交点为![]() 、
、![]() ,
,
由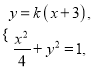 消去
消去![]() 得
得![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
, ![]() ,
,
∴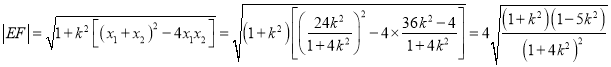 .
.
又圆![]() 的圆心
的圆心![]() 到直线
到直线![]() :
: ![]() 的距离
的距离![]() ,
,
∴圆![]() 截直线
截直线![]() 所得弦长
所得弦长![]() ,
,
∴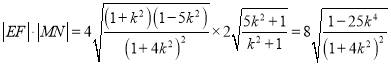 ,
,
设![]() ,
, ![]() ,
,
则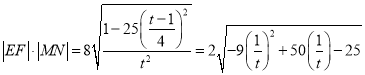 ,
,
∵![]() 的对称轴为
的对称轴为![]() ,在
,在![]() 上单调递增,
上单调递增, ![]() ,
,
∴![]() ,
,
∴![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若a=5,b=8,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.

(Ⅰ)试问:购买该商品的顾客在哪家商场中奖的可能性大?说明理由;
(Ⅱ)记在乙商场购买该商品的顾客摸到篮球的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中常数
,其中常数![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)令![]() ,将函数
,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象.区间
的图象.区间![]() 满足:
满足:![]() 在
在![]() 上至少含有30个零点.在所有满足上述条件的
上至少含有30个零点.在所有满足上述条件的![]() 中,求
中,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD= ![]() ,AB=4.
,AB=4. 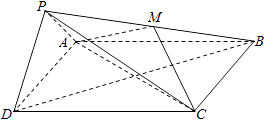
(1)求证:M为PB的中点;
(2)求二面角B﹣PD﹣A的大小;
(3)求直线MC与平面BDP所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com