【题目】在某次投篮测试中，有两种投篮方案：方案甲：先在A点投篮一次，以后都在B点投篮；方案乙：始终在B点投篮.每次投篮之间相互独立.某选手在A点命中的概率为
，命中一次记3分，没有命中得0分；在B点命中的概率为
，命中一次记2分，没有命中得0分，用随机变量
表示该选手一次投篮测试的累计得分，如果的值不低于3分，则认为其通过测试并停止投篮，否则继续投篮，但一次测试最多投篮3次.
（1）若该选手选择方案甲，求测试结束后所得分的分布列和数学期望.
（2）试问该选手选择哪种方案通过测试的可能性较大？请说明理由.
【答案】（1）数学期望为3.05，分布列见解析（2）选择方案甲
【解析】
（1）在A点投篮命中记作
,不中记作
；在B点投篮命中记作
,不中记作
，其中
，
的所有可能取值为
，即可求出
， 
， 
， 
． ，进而求出的数学期望．
（2）分别求出选手选择方案甲通过测试的概率为
，和选手选择方案乙通过测试的概率为
，比较大小，即可求出结果．
（1）在A点投篮命中记作,不中记作；在B点投篮命中记作,不中记作，
其中，
的所有可能取值为，则
，
，
，
．span>
的分布列为： 
，
，
，
．
所以
，
所以，的数学期望为
．
（2）选手选择方案甲通过测试的概率为
，
选手选择方案乙通过测试的概率为
，
因为
，所以该选手应选择方案甲通过测试的概率更大．
科目：高中数学 来源： 题型：
【题目】为了解本市的交通状况，某校高一年级的同学分成了甲、乙、丙三个组，从下午13点到18点，分别对三个路口的机动车通行情况进行了实际调查，并绘制了频率分布直方图（如图），记甲、乙、丙三个组所调查数据的标准差分别为
，则它们的大小关系为( )
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，某森林公园有一直角梯形区域ABCD，其四条边均为道路，AD∥BC，∠ADC＝90°，AB＝5千米，BC＝8千米，CD＝3千米．现甲、乙两管理员同时从
地出发匀速前往D地，甲的路线是AD，速度为6千米/小时，乙的路线是ABCD，速度为v千米/小时．
（1）若甲、乙两管理员到达D的时间相差不超过15分钟，求乙的速度v的取值范围；
（2）已知对讲机有效通话的最大距离是5千米．若乙先到达D，且乙从A到D的过程中始终能用对讲机与甲保持有效通话，求乙的速度v的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《易经》是中国传统文化中的精髓，如图是易经八卦（含乾、坤、巽、震、坎、离、艮、兑八卦），每一卦由三根线组成（"
"表示一根阳线，"
"表示一根阴线），从八卦中任取两卦，这两卦的六根线中恰有两根阳线，四根阴线的概率为_______.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两个焦点坐标分别是
、
，并且经过点
.
（1）求椭圆
的方程；
（2）若直线
与圆
：
相切，并与椭圆交于不同的两点
、
.当
，且满足
时，求
面积
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系
中，以坐标原点为极点，
轴正半轴为极轴建立极坐标系，曲线
的极坐标方程为
．
（1）
为曲线上的动点，点
在线段
上，且满足
，求点的轨迹
的直角坐标方程；
（2）设点
的极坐标为
，点
在曲线上，求
面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《九章算木》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”，现有一阳马，其正视图和侧视图是如图所示的直角三角形，该“阳马”的体积为
，若该阳马的顶点都在同一个球面上，则该球的表面积为（ ）
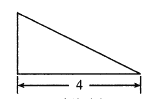
正视图 侧视图
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
