
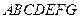 中,平面
中,平面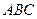 ∥平面
∥平面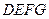 ,
,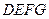 ,
,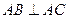 ,
,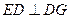 ,
,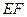 ∥
∥ .且
.且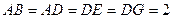 ,
, .
.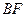 ∥平面
∥平面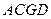 ;
; 的余弦值;
的余弦值;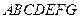 的体积.
的体积.

 ,
,
 ,所以BF∥CG.又BF
,所以BF∥CG.又BF 平面ACGD,故 BF//平面ACGD …4分
平面ACGD,故 BF//平面ACGD …4分 ,设平面BCGF的法向量为
,设平面BCGF的法向量为 ,
, ,令
,令 ,则
,则 ,
,
 =
=
 .9分
.9分 =
=
 =
= =
= .……………13分
.……………13分 平面ACGD 故 BF//平面ACGD……………4分
平面ACGD 故 BF//平面ACGD……………4分
 , ∴MN=
, ∴MN= 在直角三角形MNF中,MF=2,MN
在直角三角形MNF中,MF=2,MN
 =
= =
= =
= ,
, =
=
 …………9分
…………9分 =
= =
=
 =
= .……………13分
.……………13分

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com