
【题目】已知函数f(x)=|x﹣5|﹣|x﹣2|.
(1)若x∈R,使得f(x)≤m成立,求m的范围;
(2)求不等式x2﹣8x+15+f(x)≤0的解集.
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立坐标系.已知曲线C:ρsin2θ=2acosθ(a>0),过点P(﹣2,﹣4)的直线l的参数方程为 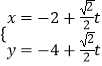 (t为参数),直线l与曲线C分别交于M、N两点.
(t为参数),直线l与曲线C分别交于M、N两点.
(1)写出曲线C和直线l的普通方程;
(2)若|PM|,|MN|,|PN|成等比数列,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一箱方便面共有50袋,用随机抽样方法从中抽取了10袋,并称其质量(单位:g)结果为:60.5 61 60 60 61.5 59.5 59.5 58 60 60
(1)指出总体、个体、样本、样本容量;
(2)指出样本数据的众数、中位数、平均数;
(3)求样本数据的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.

(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
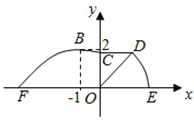
【题目】如图,某市准备在道路![]() 的一侧修建一条运动比赛道,赛道的前一部分为曲线段
的一侧修建一条运动比赛道,赛道的前一部分为曲线段![]() ,该曲线段是函数
,该曲线段是函数![]() ,
, ![]() 时的图象,且图象的最高点为
时的图象,且图象的最高点为![]() .赛道的中间部分为长
.赛道的中间部分为长![]() 千米的直线跑道
千米的直线跑道![]() ,且
,且![]() .赛道的后一部分是以
.赛道的后一部分是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
(1)求![]() 的值和
的值和![]() 的大小;
的大小;
(2)若要在圆弧赛道所对应的扇形![]() 区域内建一个“矩形草坪”,矩形的一边在道路
区域内建一个“矩形草坪”,矩形的一边在道路![]() 上,一个顶点在半径
上,一个顶点在半径![]() 上,另外一个顶点
上,另外一个顶点![]() 在圆弧
在圆弧![]() 上,且
上,且![]() ,求当“矩形草坪”的面积取最大值时
,求当“矩形草坪”的面积取最大值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.极坐标系中方程ρ2﹣4ρcosθ=0和ρ﹣4cosθ=0表示的是同一曲线
B.![]()
C.不等式|a+b|≥|a|﹣|b|等号成立的条件为ab≤0
D.在极坐标系中方程 ![]() 表示的圆和一条直线.
表示的圆和一条直线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x1 , x2 , x3 , x4 , x5满足0<x1<x2<x3<x4<x5
(1)求证不等式x12+x22+x32+x42+x52>x1x2+x2x3+x3x4+x4x5+x5x1
(2)随机变量X取值 ![]() 的概率均为
的概率均为 ![]() ,随机变量Y取值
,随机变量Y取值 ![]() 的概率也均为
的概率也均为 ![]() ,比较DX与DY大小关系.
,比较DX与DY大小关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com