
【题目】已知函数![]() ,
, ![]() 为自然对数的底数,
为自然对数的底数, ![]() .
.
(1)试讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当![]() 时,
时, ![]() 在
在![]() 上单调递增;当
上单调递增;当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2) ![]() .
.
【解析】试题分析:(1)对函数求导,关注定义域,对参数 a进行讨论,得出函数的单调性;(2)解决恒成立的最基本方法就是分离参数,化为![]() 对
对![]() 时恒成立.设右边为函数g(x),通过两次求导研究函数g(x)的单调性和最大值,最后利用极值原理得出a的范围.
时恒成立.设右边为函数g(x),通过两次求导研究函数g(x)的单调性和最大值,最后利用极值原理得出a的范围.
试题解析:
(1)![]() 的定义域为
的定义域为![]() ,
, ![]() .
.
若![]() 时,则
时,则![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
若![]() 时,则由
时,则由![]() ,∴
,∴![]() .
.
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,∴
,∴![]() 在
在![]() 上单调递减.
上单调递减.
综上所述,当![]() 时,
时, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)由题意得: ![]() 对
对![]() 时恒成立,
时恒成立,
∴![]() 对
对![]() 时恒成立.
时恒成立.
令![]() ,(
,( ![]() ),
),
∴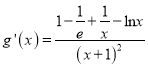 .
.
令![]() ,
,
∴![]() 对
对![]() 时恒成立,
时恒成立,
∴![]() 在
在![]() 上单调递减,
上单调递减,
∵![]() ,
,
∴当![]() 时,
时, ![]() ,∴
,∴![]() ,
, ![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时, ![]() ,∴
,∴![]() ,
, ![]() 在
在![]() 上单调递减.
上单调递减.
∴![]() 在
在![]() 处取得最大值
处取得最大值![]() ,
,
∴![]() 的取值范围是
的取值范围是![]() .
.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知圆锥曲线![]() (
(![]() 为参数)和定点
为参数)和定点![]() ,
,![]() 、
、![]() 是此圆锥曲线的左、右焦点,以原点
是此圆锥曲线的左、右焦点,以原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求直线![]() 的直角坐标方程;
的直角坐标方程;
(2)经过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交此圆锥曲线于
交此圆锥曲线于![]() 、
、![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲乙两人玩猜数字游戏,先由甲心中任想一个数字记为![]() ,再由乙猜甲刚才想的数字,把乙猜的数字记为
,再由乙猜甲刚才想的数字,把乙猜的数字记为![]() ,且
,且![]() 、
、![]() .若
.若![]() ,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
,则称甲乙“心有灵犀”.现任意找两人玩这个游戏,则二人“心有灵犀”的概率为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用![]() ,
,![]() ,
,![]() 表示空间中三条不同的直线,
表示空间中三条不同的直线,![]() 表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若![]() ,
,![]() , 则
, 则![]() ∥
∥![]() ; ② 若
; ② 若![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ;
;
③ 若![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ; ④ 若
; ④ 若![]()
![]()
![]() ,
,![]()
![]()
![]() , 则
, 则![]() ∥
∥![]() .
.
其中真命题的序号是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校举行了一次安全教育知识竞赛,竞赛的原始成绩采用百分制.已知高三学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见表.
内,发布成绩使用等级制,各等级划分标准见表.
原始成绩 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | 优秀 | 良好 | 及格 | 不及格 |
为了解该校高三年级学生安全教育学习情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
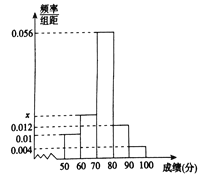
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高三学生中任选3人,求至少有1人成绩是及格以上等级的概率;
(3)在选取的样本中,从原始成绩在80分以上的学生中随机抽取3名学生进行学习经验介绍,记![]() 表示抽取的3名学生中优秀等级的学生人数,求随机变量
表示抽取的3名学生中优秀等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱载堉(1536—1611),明太祖九世孙,音乐家、数学家、天文历算家,在他多达百万字的著述中以《乐律全书》最为著名,在西方人眼中他是大百科全书式的学者王子。他对文艺的最大贡献是他创建了“十二平均律”,此理论被广泛应用在世界各国的键盘乐器上,包括钢琴,故朱载堉被誉为“钢琴理论的鼻祖”。“十二平均律”是指一个八度有13个音,相邻两个音之间的频率之比相等,且最后一个音频率是最初那个音频率的2倍,设第二个音的频率为![]() ,第八个音的频率为
,第八个音的频率为![]() ,则
,则![]() 等于
等于
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
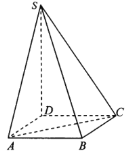
【题目】如图,四棱锥![]() 的底面是正方形,
的底面是正方形, ![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是
是![]() 上的点,且
上的点,且![]() .
.
(1)求证:对任意的![]() ,都有
,都有![]() .
.
(2)设二面角C-AE-D的大小为![]() ,直线BE与平面
,直线BE与平面![]() 所成的角为
所成的角为![]() ,
,
若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com