
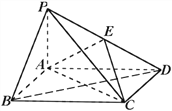
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() 面
面![]() ,
, ![]() 为
为![]() 的中点。
的中点。
(1)证明: ![]() 平面
平面![]() ;
;
(2)设![]() ,
, ![]() ,三棱锥
,三棱锥![]() 的体积
的体积 ![]() ,求A到平面PBC的距离。
,求A到平面PBC的距离。
【答案】(1)证明见解析 (2) ![]() 到平面
到平面![]() 的距离为
的距离为![]()
【解析】试题分析:(1)连结BD、AC相交于O,连结OE,则PB∥OE,由此能证明PB∥平面ACE.(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能求出A到平面PBD的距离
试题解析:(I)设BD交AC于点O,连结EO。
因为ABCD为矩形,所以O为BD的中点。
又E为PD的中点,所以EO∥PB
又EO![]() 平面AEC,PB
平面AEC,PB![]() 平面AEC
平面AEC
所以PB∥平面AEC。
(II)![]()
由![]() ,可得
,可得![]() .
.
作![]() 交
交![]() 于
于![]() 。
。
由题设易知![]() ,所以
,所以![]()
故![]() ,
,
又![]() 所以
所以![]() 到平面
到平面![]() 的距离为
的距离为![]()
法2:等体积法
![]()
由![]() ,可得
,可得![]() .
.
由题设易知![]() ,得BC
,得BC![]()
假设![]() 到平面
到平面![]() 的距离为d,
的距离为d,
又因为PB=![]()
所以![]()
又因为![]() (或
(或![]() ),
),
![]() ,
,
所以![]()


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率是
的离心率是![]() ,且过点
,且过点![]() .直线
.直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)求![]() 的面积的最大值;
的面积的最大值;
(Ⅲ)设直线![]() ,
, ![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,
, ![]() .判断
.判断![]() ,
, ![]() 大小关系,并加以证明.
大小关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,离心率为
,离心率为![]() ,动点
,动点![]() .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)求以![]() 为直径且被直线
为直径且被直线![]() 截得的弦长为2的圆的方程;
截得的弦长为2的圆的方程;
(Ⅲ)设![]() 是椭圆的右焦点,过点
是椭圆的右焦点,过点![]() 作
作![]() 的垂线与以
的垂线与以![]() 为直径的圆交于点
为直径的圆交于点![]() ,证明:线段
,证明:线段![]() 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,丨φ丨< ![]() )的部分图象如图所示,则f(x)的解析式为( )
)的部分图象如图所示,则f(x)的解析式为( ) 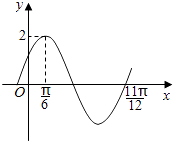
A.f(x)=2sin(x+ ![]() )
)
B.f(x)=2sin(2x+ ![]() )
)
C.f(x)=2sin(2x﹣ ![]() )
)
D.f(x)=2sin(4x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
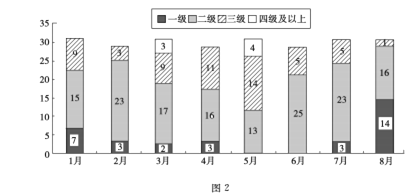
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com