练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知O是△ABC内任意一点,连结AO、BO、CO并延长交对边于A′、B′、C′,则       .

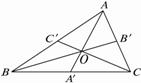
           这是平面几何中的一道题,其证明常采用“面积法”:

          

           ==1.

           运用类比,猜想对于空间中的四面体A—BCD,存在什么类似的结论?并用“体积法”证明.

           猜想:已知点O为四面体A—BCD内任意一点,连结AO、BO、CO、DO并延长交相对面于

    A′、B′、C′、D′,则有=1.?

          

    证明:设点A、O到平面BCD的距离分别为h、h′,则,?

           ∴.?

           同理,,?

           ,?

           ?

           ∴==1.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知A，B，C是平面上不共线的三点，o为平面ABC内任一点，动点P满足等式
    OP
    =
    1
    3
    [(1-λ)
    OA
    +(1-λ)
    OB
    +(1+2λ)
    OC
    ](λ∈R    且λ≠1，则P的轨迹一定通过△ABC的（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A，B，C是平面上不共线的三点，O为平面ABC内任一点，动点P满足等式
    OP
    =
    1
    3
    [（1-λ）
    OA
    +（1-λ）
    OB
    +（1+2λ）
    OC
    ]（λ∈R且λ≠0），则点P的轨迹一定通过△ABC的
    重心
    重心
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知A，B，C是平面上不共线的三点，O为平面ABC内任一点，动点P满足等式
    OP
    =
    1
    3
    [（1-λ）
    OA
    +（1-λ）
    OB
    +（1+2λ）
    OC
    ]（λ∈R且λ≠0），则点P的轨迹一定通过△ABC的______．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖北省天门市部分重点中学联考高三（上）期中数学试卷（解析版） 题型：填空题

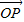    已知A，B，C是平面上不共线的三点，O为平面ABC内任一点，动点P满足等式=[（1-λ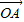）+（1-λ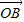）+（1+2λ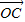）]（λ∈R且λ≠0），则点P的轨迹一定通过△ABC的    ．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年湖南省长沙市浏阳一中高三（下）第三次月考数学试卷（理科）（解析版） 题型：选择题

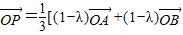
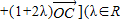    已知A，B，C是平面上不共线的三点，o为平面ABC内任一点，动点P满足等式且λ≠1，则P的轨迹一定通过△ABC的（ ）
    A．内心
    B．垂心
    C．重心
    D．外心

    查看答案和解析>>

    同步练习册答案