Question

已知数列{a_n}满足：．
（1）求证：?n∈N^*，?m_n∈N，使a_n=4m_n+3；
（2）求a₂₀₁₀的末位数字．

Answer 1

解：（1）当n=1时，a₁=3，假设n=k时，a_k=4m_k+3，m_k∈N．当n=k+1时，a_{k+1}=3^{a_{k}}=3^{4m_{k}+3}=(4-1)^{4m_{k}+3}={C}{⁰_{4m_{k}+3}}4^{4m_{k}+3}•(-1)⁰+{C}{¹_{4m_{k}+3}}•4^{4m_{k}+2}•(-1)¹++{C}{^{4m_{k}+2}_{4m_{k}+3}}•4¹•(-1)^{4m_{k}+2}+{C}{^{4m_{k}+3}_{4m_{k}+3}}•4⁰•(-1)^{4m_{k}+3}=4T-1=4（T-1）+3，其中T={C}{⁰_{4m_{k}+3}}4^{4m_{k}+2}•(-1)⁰+{C}{¹_{4m_{k}+3}}•4^{4m_{k}+1}•(-1)¹++{C}{^{4m_{k}+2}_{4m_{k}+3}}•(-1)^{4m_{k}+2}∈N^{*}∴?m_k+1=T-1∈N，使a_k+1=4m_k+1+3．∴当n=k+1时，结论也成立．∴?n∈N^*，?m_n∈N，使a_n=4m_n+3；（7分）（2）a_{n+1}=3^{a_{n}}=3^{4m_{n}+3}=(81)^{m_{k}}×27．故a₂010的末位数字是7．（10分）
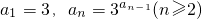