
【题目】在直角坐标系xOy中,圆C的参数方程为:![]() 为参数
为参数![]() ,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,射线l的极坐标方程为
,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,射线l的极坐标方程为![]() ,
,![]() .
.
![]() 将圆C的参数方程化为极坐标方程;
将圆C的参数方程化为极坐标方程;
![]() 设点A的直角坐标为
设点A的直角坐标为![]() ,射线l与圆C交于点
,射线l与圆C交于点![]() 不同于点
不同于点![]() ,求
,求![]() 面积的最大值.
面积的最大值.
科目:高中数学 来源: 题型:
【题目】北京地铁八通线西起四惠站,东至土桥站,全长![]() ,共设13座车站
,共设13座车站![]() 目前八通线执行2014年12月28日制订的计价标准,各站间计程票价
目前八通线执行2014年12月28日制订的计价标准,各站间计程票价![]() 单位:元
单位:元![]() 如下:
如下:
四惠 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | |
四惠东 | 3 | 3 | 3 | 4 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | ||
高碑店 | 3 | span>3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | |||
传媒大学 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | ||||
双桥 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 4 | |||||
管庄 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | ||||||
八里桥 | 3 | 3 | 3 | 3 | 4 | 4 | |||||||
通州北苑 | 3 | 3 | 3 | 3 | 3 | ||||||||
果园 | 3 | 3 | 3 | 3 | |||||||||
九棵树 | 3 | 3 | 3 | ||||||||||
梨园 | 3 | 3 | |||||||||||
临河里 | 3 | ||||||||||||
土桥 | |||||||||||||
四惠 | 四惠东 | 高碑店 | 传媒大学 | 双桥 | 管庄 | 八里桥 | 通州北苑 | 果园 | 九棵树 | 梨园 | 临河里 | 土桥 |
![]() 1
1![]() 在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
在13座车站中任选两个不同的车站,求两站间票价为5元的概率;
![]() 2
2![]() 在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
在土桥出站口随机调查了n名下车的乘客,将在八通线各站上车情况统计如下表:
上车站点 | 通州北苑
| 双桥 | 四惠
|
频率 |
| a | b |
人数 | c | 15 | 25 |
求a,b,c,n的值,并计算这n名乘客乘车平均消费金额;
![]() 3
3![]() 某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车
某人从四惠站上车乘坐八通线到土桥站,中途任选一站出站一次,之后再从该站乘车![]() 若想两次乘车花费总金额最少,可以选择中途哪站下车?
若想两次乘车花费总金额最少,可以选择中途哪站下车?![]() 写出一个即可
写出一个即可![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
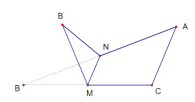
【题目】如图,∠C=![]() ,
,![]() ,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为
,M,N分别是BC,AB的中点,将△BMN沿直线MN折起,使二面角B'-MN-B的大小为![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)的焦点F,直线y=4与y轴的交点为P,与抛物线C的交点为Q,且|QF|=2|PQ|.
(1)求p的值;
(2)已知点T(t,-2)为C上一点,M,N是C上异于点T的两点,且满足直线TM和直线TN的斜率之和为![]() ,证明直线MN恒过定点,并求出定点的坐标.
,证明直线MN恒过定点,并求出定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②函数![]() ,的最小值是3
,的最小值是3
③用长为![]() 的铁丝围成--个平行四边形,则该平行四边形能够被直径为
的铁丝围成--个平行四边形,则该平行四边形能够被直径为![]() 的圆形纸片完全覆盖
的圆形纸片完全覆盖
④已知正实数![]() ,
,![]() 满足
满足![]() ,则
,则![]() 的最小值为
的最小值为![]() .
.
其中所有正确命题的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴为正半轴为极轴建立极坐标系.已知曲线
轴为正半轴为极轴建立极坐标系.已知曲线![]() 的极坐标方程为
的极坐标方程为![]()
![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 过定点
过定点![]() 且倾斜角为
且倾斜角为![]() 交曲线
交曲线![]() 于
于![]() 两点.
两点.
(1)把曲线![]() 化成直角坐标方程,并求
化成直角坐标方程,并求![]() 的值;
的值;
(2)若![]() 成等比数列,求直线
成等比数列,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 九章算术
九章算术![]() 给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除
给出求羡除体积的“术”是:“并三广,以深乘之,又以袤乘之,六而一”,其中的“广”指羡除的三条平行侧棱的长,“深”指一条侧棱到另两条侧棱所在平面的距离,“袤”指这两条侧棱所在平行线之间的距离,用现代语言描述:在羡除![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,两条平行线
,两条平行线![]() 与
与![]() 间的距离为h,直线
间的距离为h,直线![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则该羡除的体积为
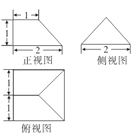
,则该羡除的体积为![]() 已知某羡除的三视图如图所示,则该羡除的体积为
已知某羡除的三视图如图所示,则该羡除的体积为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com