
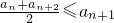 ;②an≤M,其中n∈N*,M是与n无关的常数.
;②an≤M,其中n∈N*,M是与n无关的常数. d=-n2+9n(2分)
d=-n2+9n(2分) -Sn+1=
-Sn+1= [(-n2+9n)-(n+2)2+9(n+2)+2(n+1)2-18(n+1)]=-1<0
[(-n2+9n)-(n+2)2+9(n+2)+2(n+1)2-18(n+1)]=-1<0 <Sn+1,适合条件①;
<Sn+1,适合条件①; +
+ ,所以当n=4或5时,Sn取得最大值20,即Sn≤20,适合条件②
,所以当n=4或5时,Sn取得最大值20,即Sn≤20,适合条件②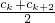 ≤ck+1,所以ck+2≤2ck+1-ck≤2(ck-1)-ck=ck--2
≤ck+1,所以ck+2≤2ck+1-ck≤2(ck-1)-ck=ck--2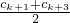 ≤ck+2,所以ck+3≤2ck+2-ck+1≤2(ck+1-1)-ck+1=ck+1-2≤ck-3
≤ck+2,所以ck+3≤2ck+2-ck+1≤2(ck+1-1)-ck+1=ck+1-2≤ck-3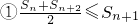 ,然后求出M使得Sn≤M②
,然后求出M使得Sn≤M②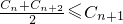 ,即
,即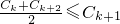 递推得到矛盾,所以说明假设错误,从而肯定结论成立.
递推得到矛盾,所以说明假设错误,从而肯定结论成立.

科目:高中数学 来源: 题型:
| an+an+2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 |
| 2 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+an+2 |
| 2 |
| 1 |
| 5 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com